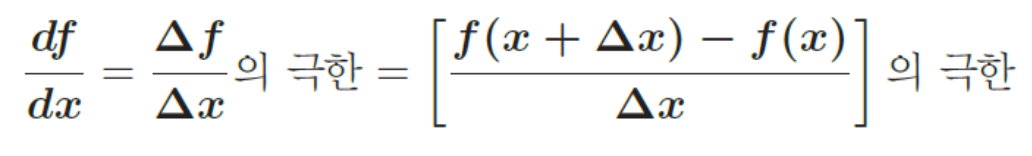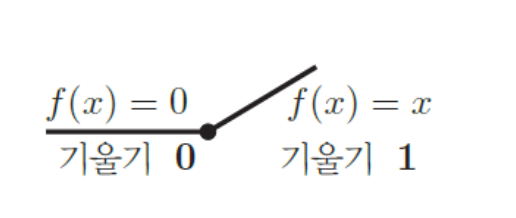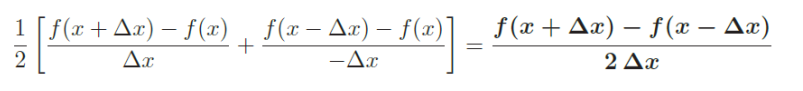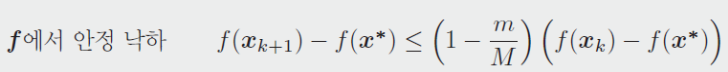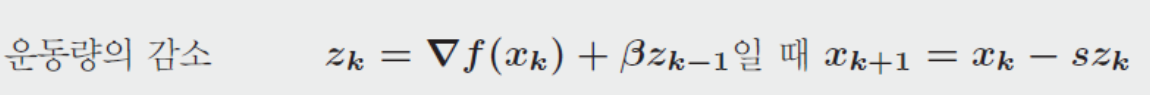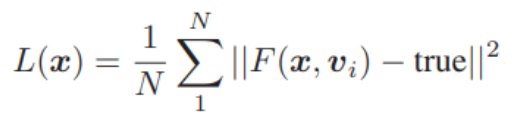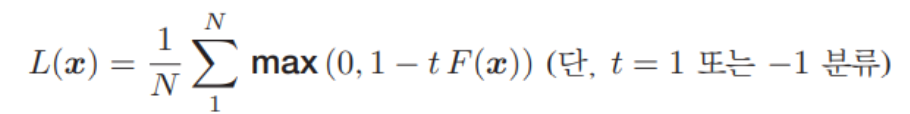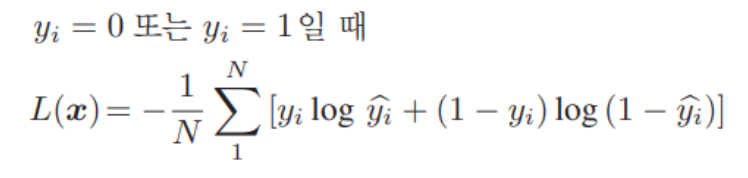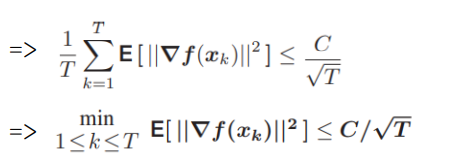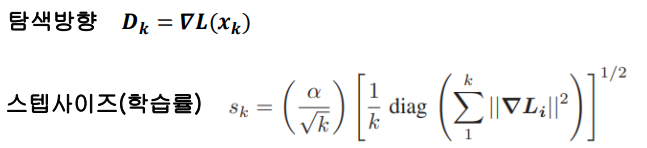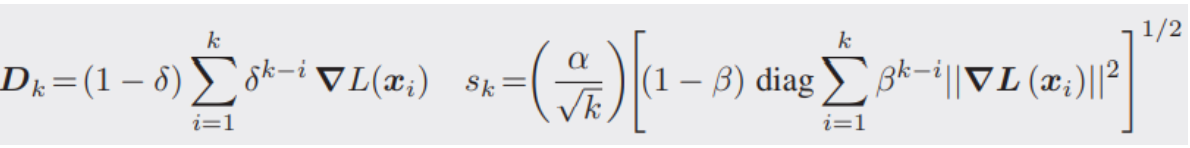최적화(Optimization) & 경사하강(Gradient Descent)에 대한 정리
최적화(Optimization) & 경사하강(Gradient Descent)에 대한 정리
이 게시글은 딥러닝을 위한 선형대수학 저서의 6장. 최적화 파트를 정리한 내용과, 추가적으로 정리한 내용으로 만들어졌습니다.
0. 최적화(Optimization)
ML, DL 분야에선 모델의 목적함수(Objective Function)인 손실 함수(Loss Function)를 최소화하기 위하여 모델의 파라미터를 학습시킨다. 이렇게 손실 함수를 최소화하기 위하여 파라미터를 학습시키는 과정을 최적화(Optimization)이라고 한다.
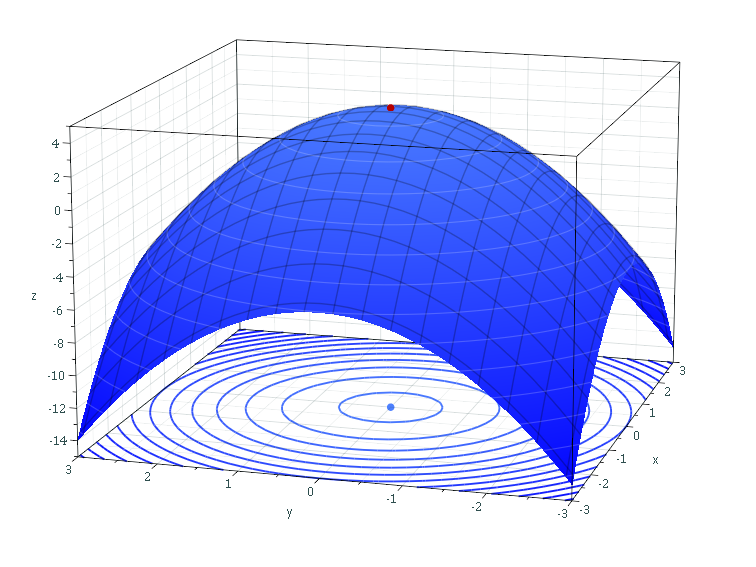
손실함수 $f(x)$가 주어졌을 때, 최적화의 목표는 함수 $f(x_1, …, x_n)$을 최소화하는 것이다. 이때, 함수 $f$는 많은 변수를 포함한다.
1. 최솟값으로 향하는 경사하강(Gradient Descent)
1-1. 근본적인 문제(Fundamental problem)
: 함수 $f(x) = f(x_1, x_2, x_3, … , x_n)$ 를 최소화하라 !
미적분학(Caculus)에서 부분적인 해결책을 제시함.
→ 매끄러운(미분 가능한) 원시함수에 대한 일계도함수가 0이 되는 지점. ($\partial f / \partial x_i = 0$)
ex ) 20개의 변량으로 이루어진 함수 $f$를 최소화하면 20개의 $\partial f/\partial fx_i = 0$ 이 생성됨.
모든 변량에 대한 이계도함수가 연속일 경우, 함수의 이계도함수를 표현하는 Hessian 행렬(대칭 행렬)로 표현 가능하다. 계산의 용이성 $\uparrow$
20개의 일계 도함수가 존재하고 계산할 수 있는, 즉 도함수가 정의되어 있는 원시함수가 20개 모두 이계도함수까지 정의된 경우는 매우 드물다.
→ 함수의 모든 변수에서 이계도함수의 존재성 보장 X.
$\therefore$ 이계도함수는 매우 유용한 추가 정보이지만 현실 조건상 많은 문제에서 이계도함수를 사용하기는 매우 힘듬.
What is the goal?
→ 우리는 함수 $f(x)$를 최소화하는 점 $x^* = argmin f$으로 이동하길 원함.
1-2. 경사 하강(Gradient Descent)
: (편)도함수 $\partial f / \partial x_i$를 사용하여 함수 $f(x)$가 감소하는 방향을 찾는다. 가장 가파른 방향은 함수 $f(x)$가 가장 빠르게 감소하는 방향, 즉 기울기 $-\nabla f$을 통해 알 수 있다.
경사하강의 과정은 다음과 같다.
최적화할 함수 $f(x)$에 대하여 먼저 시작점 $x_0$를 정한다. 현재 $x_k$가 주어졌을 때, 그 다음으로 이동할 점인 $x_{k+1}$은 다음과 같이 계산된다.
수식 : $x_{k+1} = x_k - s_k\nabla f(x_k)$ , $s_k$ : 학습률(learning rate)
학습률(learning rate)이라고 불리는 매개변수인 $s_k$는 $x_k$에서 구한 기울기 $\nabla f(x_k)$를 반영하여 $x_{k+1}$를 얼마나 이동시킬 지 조절한다.
경사하강에서 점이 이동할 때의 step size와 방향을 정하기 위해 연구자들의 많은 생각과 계산 노력 및 경험이 들었다고 한다.
1-3. 미분적분학의 관점에서 바라본 도함수와 $\nabla f$
(i) $f(x)$의 도함수(도함수의 정의)
- 대수학(Algebra)에서의 도함수 : 함수의 접선의 기울기
- 미분적분학(Calculus)에서의 도함수 : 함수의 (순간)변화율
함수 $f(x)$의 도함수는 극한을 포함한다.
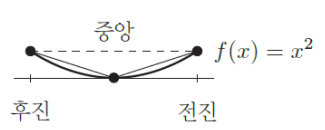
위의 식은 $\Delta x > 0$일 때 전진차분(forward difference)이고, $\Delta x < 0$ 일 때 후진차분(backward difference)이 된다.
(ii) ReLU (Ramp 함수)
신호처리, 딥러닝 분야에서 ReLU를 비롯한 Ramp함수(지니 아님) 사용.
$x=0$에서 도함수의 좌극한 ≠ 우극한이므로, 도함수 $\partial f / \partial x$ 가 존재하지 않는다.
(iii) 유심차분(Centered difference)
전진 차분(forward difference)과 후진 차분(backward difference)을 평균함으로써 극한값에 더 가까운 비율을 얻을 수 있다.
ex ) $f(x) = x^2$을 유심차분하면 정확한 도함수 $\partial f / \partial x_i$ = 2x 가 생성됨
1-4. 기울기 벡터 $\nabla f$의 기하학
함수가 이변수함수인 경우 : $f(x, y)$
$x, y$의 값이 바뀌면 $\nabla f$가 바뀐다.
||$\nabla f$|| 은 함수 $f$의 그래프의 가파른 정도를 알려준다.
가장 가파른 경사 : $\nabla f = grad f$ 방향인 경우
→ 미분의 방향성이 관건.
1-5. 가장 가파른 하강에 대한 수렴분석
함수 $f(x)$의 볼록성은 헤시안 행렬 $H=\nabla^2f$에 대한 양의 정부호 여부에 따라 결정된다.
(식1)에 $M$을 곱하고 (식2)에 $m$을 곱한 후 두 식을 빼서 $||\nabla f||^2$을 제거하면 다음 결과를 얻는다.
위 식은 매 단계마다 골짜기 밑바닥의 높이가 적어도 $c=1-m/M$만큼 감소함을 의미함.
$\therefore$ 헤시안 행렬인 이차미분계수의 상한(supremum)과 하한(infimum)이 함수의 경사 하강 속도에 큰 영향을 미친다. $m/M$이 작을 때 경사 하강의 선형 수렴(linear convergence)은 매우 느려진다.
1-6. 비정밀 선 탐색(Inexact Line Search)과 역추적법(Backtracking)
직선 $x = x_k - s\nabla f_k$ 을 따라 $x_{k+1}$는 $f(x)$를 정확히 최소화했다.
비율 $m/M$은 근사 이론과 수치선형대수학 전반에 나타난다. 최솟값에 도달하기까지의 하강 비율을 조절하는 $m/M$과 같은 수를 찾는 작업은 수학 분석의 핵심이다.
학습률 $s$를 선택하는 것은 일변수 최소화 문제이고 이 직선은 $x_k$에서 가장 가파른 하강 방향으로 움직이게 한다.
그러나 비록 선 위를 움직이더라도 일반적인 함수 $f(x)$를 최소화하는 정확한 공식은 기대할 수 없다.
따라서 근사 최솟값을 찾는 빠르고 분별력(sensible) 있는 방법이 필요하고 추가 오차에 관한 제한(bound)이 필요하다.
- 분별력(sensible) : 최솟값을 찾는 데 걸리는 시간이 짧은 것.
- 제한(bound) : 규제(regularization) 등을 통한 오차의 크기 제한.
- 역추적법(backtracking) - One of sensible method
함수 그래프의 곡면의 특성에 맞춰 학습률을 적응적으로 선택하는 방법.
1-7. Momentum과 Path
물리학에서 착안한 아이디어
Key idea :
언덕에서 무거운 공이 구를 때 지그재그가 나타나지 않는다. 무거운 공의 운동량(momentum)은 좁은 골짜기를 통해 공을 운반한다. 측면에 부딪히더라도 대부분 앞으로 향한다.
→ Local minimum에 빠져도 momentum을 이용해 빠져나온다.
위의 수식을 따라 각 step마다의 momentum을 계산하여 학습에 적용한다.
1-8. Nesterov Acceleration
유리 네스테로프(Yuri Nesterov)가 제안함.
1-9. 함수 최소화의 큰 그림
볼록성과 기울기를 기준으로 함수 $f(x)$의 성질을 분류하면 다음과 같다.
- 볼록성 : 순볼록(strictly convex), 간신히(barely) 볼록, 볼록이 아님
- 기울기 : 선형(linear), 비선형(non-linear)
함수의 성질에 따른 문제의 난이도 순으로 유형을 나열하면 다음과 같다.
- $f(x, y) = 1/2(x^2 + by^2)$ (strictly convex)
- $f(x_1, … , x_n) = 1/2x^TSx - c^Tx$ (strictly convex)
- $f(x_1, … , x_n)$ = (매끄러운 순볼록 함수)(smooth strictly convex function)
- $f(x_1, … , x_n)$ = (순볼록이 아닌 볼록함수) (convex function)
헤시안 행렬 $H$의 고윳값의 수, $\nabla f$의 선형성 여부에 따른 난이도 변화가 존재한다.
1-10. 제약조건과 근위점(Proximal Points)
우선, Convex set이란?
→ 어떤 집합에 속한 임의의 두 점을 연결한 선분이 언제나 이 집합 안에 속하는 경우, 이 집합을 볼록집합(convex set)이라 한다.
가장 가파른 하강에서 $x$를 볼록집합(convex set) $K$로 제한하는 제약 조건을 처리하는 방법을 알아보자.
$K$ 위로의 사영
→ $x_1, x_2$를 convex set 위로 사영(projection)하면, 두 위상의 차이는 기존보다 작거나 같다.
근위 함수
→ 원본 목적함수를 미분 가능한 함수와 미분 불가능한 함수로 분리한다.
$f$$(x) = g(x) + h(x)$로 분리할 때, 두 함수 $g$와 $h$는 다음과 같은 성질을 같는다.
- $g$는 convex이고 미분 가능하다.
- $h$는 convex이고 미분 불가능하다.
사영 경사하강
→ convex set 밖에서 경사 하강 진행한 후 convex set 위로 사영하기.
근위 경사하강
→ $f$가 미분 가능하지 않다면 경사하강을 진행할 수 없다. 그러므로 $f$를 $g+h$로 나누어 미분 가능한 $g$를 이차식으로 근사, 미분 불가능한 $h$의 값을 작아지도록 위치를 조정한다.
근위 경사하강에 대한 참고 링크 :
2 확률적 경사하강(Stochastic Gradient Descent)과 ADAM
2-1. 고전적 경사 하강(Gradient descent)의 한계
- 모든 강하 단계에서 $\nabla L$을 계산하는데 너무 많은 비용이 듬. 총 손실 $L$은 훈련 집합의 모든 표본 $v_i$에 대해 개별 손실을 더한 것으로 $L$의 모든 계산을 위해서는 잠재적으로 수백만 개의 개별 손실이 계산되고 더해짐. → 매 step마다 전체 데이터의 손실함수를 계산해야 한다.
- 가중치의 수는 훨씬더 많음. 즉 $\nabla_x L = 0$을 만족하는 가중치 $x^*$가 많을 수 있음. 이러한 선택 중 일부는 학습에 사용되지 않은 validation/test 데이터에 대해 만족스럽지 않은 결과를 제공할 수도 있음. 따라서 학습 함수(learning funciton) $F$는 “일반화(generalization)”에 실패할 수 있음. → 경사하강의 결과가 local minimum이 될 수 있음.
2-2. 확률적 경사하강(SGD)의 의의
Let. 전체 훈련 데이터를 mini batch로 쪼갠다. 각 step에서 mini batch 중 하나를 무작위(stochastic)로 추출하여 학습에 사용한다.
→ 전체 배치(full batch)를 미니 배치(mini batch)로 대체 step 횟수를 $B$라고 할 때, 손실함수 $L(x)$는 손실 $B$개의 합으로 변경된다.
이 과정을 통해 고전적 경사 하강의 두 가지 문제점이 해결됨.
How?
- mini batch를 이용한 훈련 과정에서 step마다 필요한 계산 횟수 대폭 감소
- 전체 데이터(full batch data)의 편향(bias)을 따를 확률 감소. 즉 generalization error가 감소한다. → local minimum에 빠질 가능성 감소
과한 학습 진행 시(step 횟수를 많게 선언한 경우) 모델이 훈련 데이터에 과적합(overfitting)되어 generalization erorr가 다시 증가할 수 있다.
→ 조기종료(early stopping)을 통한 과적합 방지
2-3. 손실함수(Loss Function)와 학습함수(Learning Function)
어떤 함수를 최적화해야 하는가? (목적함수)
신경망에서 자주 사용되는 손실함수의 종류
제곱 손실(square loss)
힌지 손실(hinge loss)
교차엔트로피 손실(cross-entropy loss)
$F$는 각 데이터 벡터 $v$를 분류하는 학습함수이며 선형 또는 비선형임. $N$은 샘플 사이즈이고 만약 크기가 $B$인 미니배치에서 $N$은 $B$로 교체됨
SGD는 한 번의 학습 step에서 mini batch를 이용하므로, full batch를 이용할 때 보다 많은 학습 step이 진행되어야 한다.
온라인 자료에 따르면 한 번의 학습에서 사용하는 mini batch의 크기는 $B ≤ 32$를 선택하는 것이 좋음.
batch size에 대한 고찰 온라인 자료 :
2-4. 반수렴(Semi-convergence)
SGD의 전형적인 특징은 시작시 빠른 수렴을 하는 “반수렴(semi-convergence)”이다.
- 반수렴이란?
: 초기 step에서 최솟값을 향해 빠르게 이동하지만, 이후의 SGD반복은 자주 불규칙하다는 것임. step을 진행할수록 좌표는 최솟값 근처에서 큰 진동으로 변함.
이유는? mini-batch들의 경향성의 변화가 크게 일어나기 때문.
이 문제에 대한 한 가지 대응은 수렴을 일찍 멈춰 데이터가 과대적합되는 것을 방지하는 것임. ex) 조기종료
2-5. 무작위 카츠마르츠(Kaczmarz) 방법
- 카츠마르츠 방법이란?
선형 방정식 시스템(Linear Equation System) ($Ax=b$ , $A$는 $a_1$, $a_2, a_3,…,a_i$의 equation으로 이루어져 있는 시스템.)을 풀기 위한 반복 알고리즘 → 사영(projection)을 이용
- 무작위 카츠마르츠 방법
선형 방정식 시스템의 equation 중 하나를 확률에 비례하여 무작위로 선택한 후 반복 사영 진행.
*확률 : $||a_i||^2$에 비례.
2-6. 기댓값 수렴(Convergence in Expectation)
무작위로 데이터를 선택하여 학습을 진행할 때 최적점에 수렴할 수 있는지에 대한 증명 필요 → 수브리트 스라(Suvrit Sra)가 증명.
증명 과정 재현
함수 $f(x)$는 $(1/n)\sum f_i(x)$의 $n$개 항의 합과 같다. 샘플은 $1$에서 $n$까지 수 중 $k$단계에서 (교체를 포함하여) 균등하게 $i(k)$를 선택한다.
전제조건
- step size $s$ = $(상수) / \sqrt T$
- $f(x)와 \nabla f(x)$에 대해 가정하고, 랜덤 추출에 대한 편향이 없음.
가정 1 : $\nabla f(x)$의 립시츠(Lipschitz) 상수의 매끄러움 : $||\nabla f(x) - \nabla f(y)|| ≤ L||x-y||$
가정 2 : 기울기의 경계 : $||\nabla f_{i(k)} (x)|| ≤ G$
가정 3 : 불편된(unbiased) 확률적 경사 : $E[\nabla f_{i(k)}(x) - \nabla f(x)] = 0$
가정 1에 따르면 다음 결과를 얻는다.
$f(x_{k+1}) ≤ f(x_k) + (\nabla f(x_k), x_{k+1} - x_k) + 1/2Ls^2||\nabla f_{i(k)}(x_k)||^2$
$f(x_{k+1}) ≤ f(x_k) + (\nabla f(x_k), -s\nabla f_{i(k)}(x_k)) + 1/2Ls^2||\nabla f_{i(k)}(x_k)||^2$
이제 양변에 기댓값을 취하고 가정 2와 가정 3 사용.
$E[f(x_{k+1}) ≤ E[f(x_k)]-sE[||\nabla f(x_k)||^2] + 1/2Ls^2G^2$
⇒ $E[||\nabla f(x_k)||^2]≤1/sE[f(x_k) - f(x_{k+1})] + 1/2Ls^2G^2$
step size를 $s = c/\sqrt T$ 로 선택하고, $k=1$부터 $T$까지 위의 식의 합을 구하자.
$\therefore$ SGD를 비롯한 경사하강은 목적함수의 최솟값을 찾는 과정. random하게 선택된 mini-batch들로 학습하여 계산한 목적함수의 최솟값의 supremum을 보여 수렴성을 증명하였다.
2-7. 확률적 가중치 평균화(Stochastic Weight Averaging)
https://arxiv.org/abs/1803.05407
- summary
SGD의 과정에서 각 step마다 최적화한 가중치를 평균화하여 학습을 진행하는 것이 generalization에 대한 성능과 향상과 overhead의 비용이 감소한다.
2-8. 초기 기울기를 사용한 적응법(Adaptive Method)
GD, SGD를 사용해 보면 결과가 수렴하지 않거나 매우 오랜 step에 걸쳐 수렴하는 경우가 있다. 이런 경우 더 빠른 수렴을 위해 적응법(adaptive method)이 주로 사용되어 왔다.
적응법(Adaptive)의 아이디어 : 이전 단계의 기울기 사용(memory)
이러한 “메모리(memory)”는 탐색 방향 $D$와 stepsize(학습률) $s$를 선택하는 데 중요한 지표가 될 수 있다.
Q) 손실함수 $L(x)$를 최소화하는 벡터 $x^*$를 찾아보자!
$x_k$에서 $x_{k+1}$까지의 단계에서, $D_k$와 $s_k$는 자유롭게 선택할 수 있음.
기존의 표준 SGD에서 $D_k$는 현재 기울기 $\nabla L_k(x_k, B)$에만 의존하고 $s_k = s/\sqrt k$임. 여기서 오로지 실험 데이터 $B$의 무작위 미니배치로 평가됨.
심층 신경망(deep networks)은 종종 이전 기울기 중 일부 또는 전체를 사용하고 기울기는 초기의 무작위 미니배치에서 계산되었다.
성공과 실패는 $D_k$와 $s_k$에 달려있다. $D_k$와 $s_k$의 선택에 따른 여러 모형이 고안되고 있다.
ADAGRAD (Adaptive Gradient Algorithm)
$\alpha / \sqrt{k}$ 는 SGD의 수렴성 증명에서 대표적으로 감소하는 stepsize로 실제로 천천히 수렴할 때 종종 생략된다.
파라미터 별로 학습 정도에 따라 다른 step size 적용.
- 학습이 많이 된 파라미터는 step size 감소
- 학습이 적게 된 파라미터는 step size 증가
위 식에서 ‘메모리 인자’는 수렴 속도에서 실제적인 상승을 이끈다.
ADAM (Adaptive Moment Estimation Algorithm) Momentum + RMSProp
ADAM의 결점
ADAM 알고리즘이 세 단계마다 잘못된 방향으로 두 번, 옳은 방향으로 한 번씩 가는 문제가 발생.
ADAM의 수렴이 실패하면 항상 볼록 최적화 문제(convex optimization)가 발생한다.
ADAM을 보완하기 위한 하나의 접근법
→ 학습에 사용되는 미니배치의 크기를 점점 증가시킨다. : YOGI. 개선된 결과를 보여줌.
YOGI 관련 논문 링크 :
https://papers.nips.cc/paper_files/paper/2018/file/90365351ccc7437a1309dc64e4db32a3-Paper.pdf
2-9. 일반화(Generalization) : 딥러닝이 어려운 이유
일반화는 새로운 실험 데이터에 대한 신경망의 행위를 말한다.
Question :
**알려진 훈련 데이터 $v$를 성공적으로 분류하는 함수 $F(x, v)$를 구성하면, $F$는 $v$가 훈련 데이터 밖에 있을 때도 계속 정확한 결과를 제공할까?</span**
→ 이 질문의 답은 가중치를 선택하는 SGD 알고리즘에 달려있다. 가중치 $x$는 훈련 데이터에 대한 손실함수 $L(x, v)$를 최소화한다.
$v$의 데이터보다 $x$의 파라미터가 많은 경우가 자주 존재한다. 이 경우 우리는 많은 가중치 집합(많은 벡터 $x$)의 구성이 훈련 집합에서도 동일하게 정확할 것으로 예상할 수 있다. 가중치는 좋고 나쁠 수 있으며, generalization이 잘 될 수도 있고 잘 되지 않을 수도 있다. 알고리즘은 특정한 $x$를 선택하고, 이 가중치를 새로운 데이터 $v_{test}$에 적용한다.
다음 Question :
train에서 계산된 가중치가 test/valid 데이터에서 잘 작동하는 이유는 무엇인가?
→ 특이한 실험 - 각 입력 벡터 $v$의 성분이 무작위로 폐기되었다. 그래서 $v$로 표현되는 개별 특징은 갑자기 어떤 의미도 가지지 못하게 되었다(편향성 삭제). 그럼에도 불구하고 심층 신경망은 무작위로 추출한 샘플을 학습했다. 학습함수 $F(x, v)$는 여전히 실험 데이터를 정확히 분류했다.
물론 $v$의 성분이 다시 정렬되었을 때, $F$는 처음 보는 데이터에 대하여 성공할 수 없었다.
Dropout을 통한 규제(Regularization)를 이용한 과적합 방지