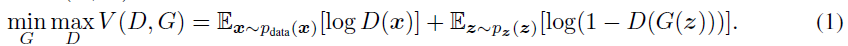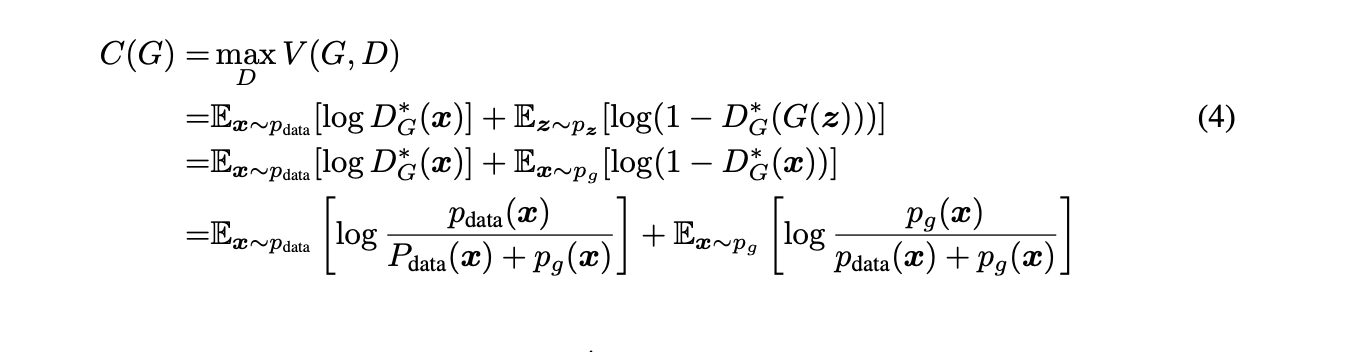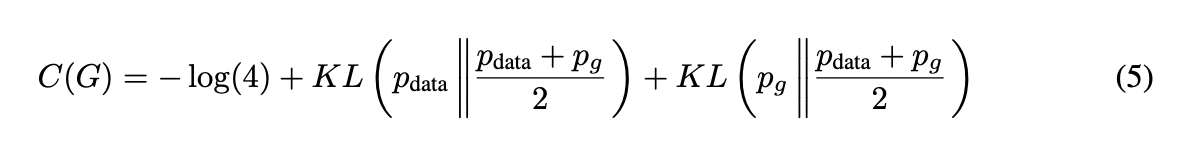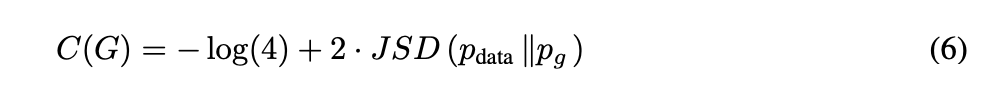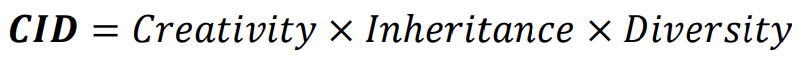GAN (Generative Adversarial Networks) 논문 리뷰 & How to evaluate GANs?

GAN (Generative Adversarial Networks) 논문 리뷰 & How to evaluate GANs?

0. 이미지 데이터의 확률 분포와 생성 모델

이미지 데이터는 벡터나 행렬과 같은 데이터의 형태로 표현하여 컴퓨터가 연산을 진행할 수 있다. 이미지 데이터는 일반적인 일차원 데이터와 달리 RGB와 같은 여러 개의 채널로 이루어져 다차원 특징 공간 상의 한 점으로 표현된다.

이러한 고차원 공간 상에 존재하는 이미지 데이터의 다변수 확률 분포를 학습하여 근사하는 모델을 학습할 수 있다. 학습을 진행한 결과 사람의 얼굴에도 통계적인 평균치가 존재할 수 있다. 모델은 이를 수치적으로 표현할 수 있게 된다.

생성 모델(Generative model)은 주어진 학습 데이터를 학습하여 학습 데이터의 분포를 따르는 유사한 데이터를 생성하는 모델이다. 쉽게 말하자면 실존하지 않지만 있을 법한 이미지를 생성하는 모델을 의미한다.

생성 모델의 목표는 주어진 이미지 데이터의 분포를 최대한 잘 근사(approximate)하는 것이다. 생성 모델이 잘 동작한다는 것은 원래 이미지들의 분포를 잘 모델링한다는 것을 의미한다. 생성 모델의 학습이 잘 되었다면 통계적으로 평균적인 특징을 가지는 데이터를 쉽게 생성할 수 있게 된다.

1. Introduction

딥러닝의 목표는 인공지능을 활용하는 데 있어 마주치는 모든 타입의 데이터들을 확률 분포로 표현하는 풍부하고 계층적인 모델을 만들어내는 것이다. 예를 들어 자연 이미지, 스피치를 포함한 오디오 파형, 자연어 말뭉치(corpos) 등이 있다.

이러한 딥러닝 모델 중 가장 성공적이였던 모델은 discriminative model(구별 모델)이다. 이 모델은 고차원이면서 많은 정보가 담긴 입력 데이터의 클래스의 label을 mapping하는 것이다. discriminative model은 역전파(backpropagation)와 드롭아웃(dropout)을 기반으로 하고, well-behaved gradient를 갖는 piecewise linear unit(ex: ReLU activation function)을 이용하여 많은 성공을 거두었다.

컴퓨터로 정확한 계산이 어려워 근사적으로 계산하여야 하는 최대우도법(MLE)와 같은 확률적 근사 계산의 어려움 때문에 지금껏 Deep generative model(깊은 생성 모델)은 큰 성과를 내지 못하였고, piecewise linear unit을 활용함에 있어서 생기는 이점을 생성 모델의 환경에서 사용하는 것의 어려움 또한 존재하였다.

본 논문에서는 상기한 단점을 피하는 새로운 생성 모델을 제안한다.

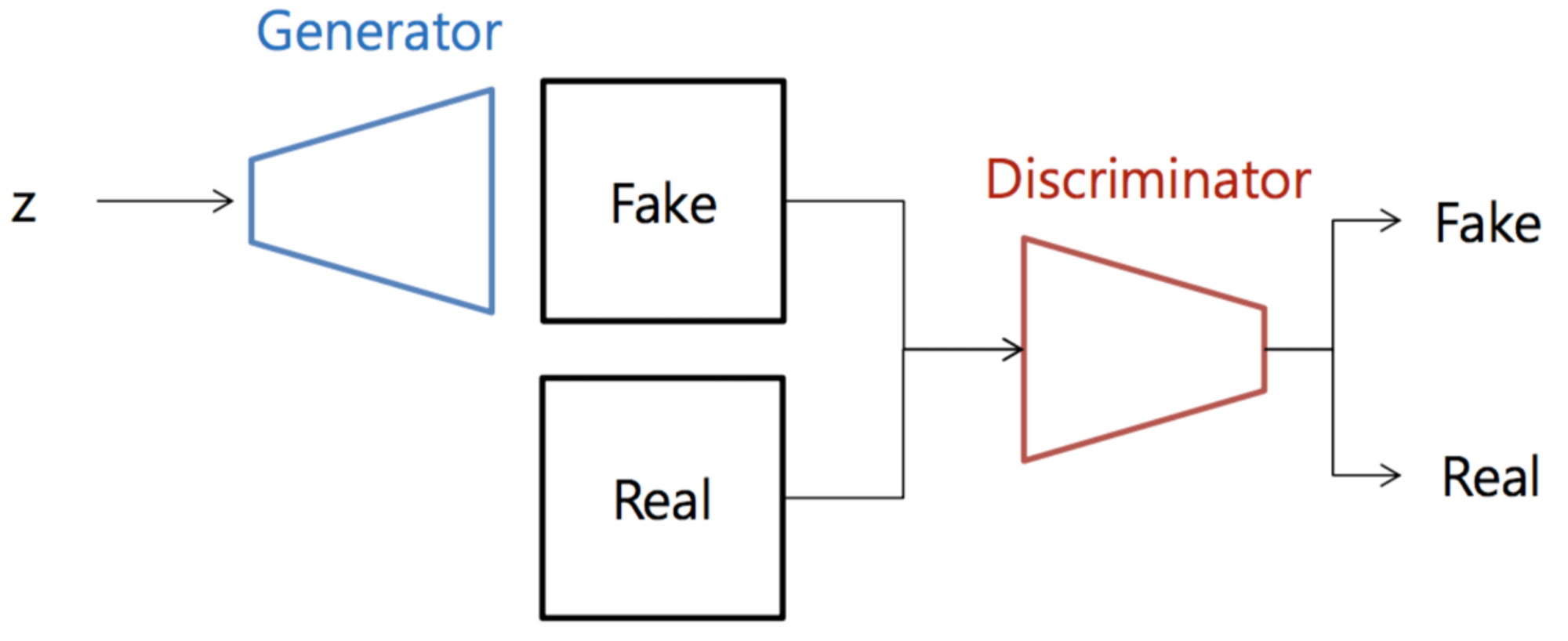
논문에서 제안하는 adversarial nets framework에서는 generative model이 adversary model과 적대하여 학습을 진행한다. discriminative model은 입력된 샘플이 원본 데이터인지 생성 모델이 만들어낸 것인지 구별하도록 학습을 진행하게 된다.

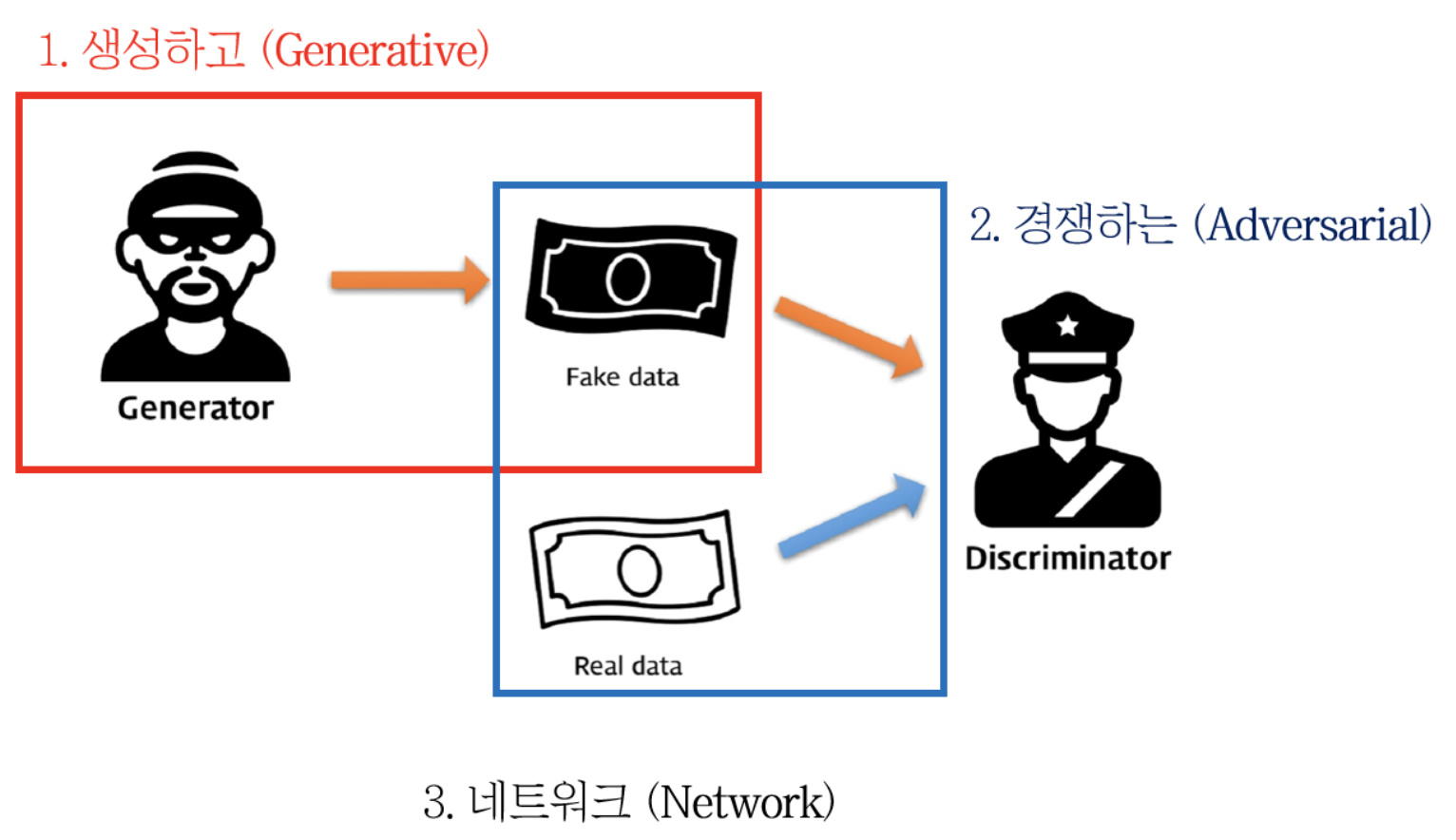
이것은 마치 경찰과 위조 지폐범의 경쟁으로 비유될 수 있다. generative model은 생성자(generator)로 경찰을 속이도록 최대한 비슷한 위조 지폐를 만들어야 하는 위조 지폐범, discriminative model은 판별자(discriminator)로 생성자가 만든 위조 지폐와 진짜 지폐를 구별해야 하는 경찰관으로 생각할 수 있다.

이러한 경쟁 방식은 생성자와 판별자 모두에게 각자의 성능을 최대한으로 끌어올리도록 유도할 수 있다.

이런 적대적 생성 프레임워크는 수많은 훈련 모델과 최적화 알고리즘을 이끌어낼 수 있다.

이번 논문에서는 생성 모델이 MLP(Multi perceptron layer)를 통하여 random noise가 추가된 인풋을 이용하여 생성해낸 샘플을 채택하여 탐구를 진행하였다. 그리고 구별 모델 또한 MLP로 이루어져 있다.

우리는 이러한 특수 케이스를 적대적 신경망(adversarial nets)이라고 칭하기로 했다. 적대적 신경망에서는 드롭아웃과 역전파 알고리즘을 이용하여 두 모델의 학습을 진행하고, 생성 모델은 순전파 알고리즘만을 이용하여 샘플 제작을 진행하였다.

이 과정에서 마르코프 체인과 근사를 통한 추론과정은 없어도 된다.

2. Adversarial Nets

적대적 모델링 네트워크는 각 모델이 MLP로 이루어졌을 경우 가장 간단하다.

생성자의 데이터 $x$에 대한 분포 $p_g$를 학습하려 할 때, 우리는 먼저 input noise 변수의 사전 분포인 $p_z(z)$를 정의한 뒤 데이터 공간의 매핑 $G(z;\theta_g)$를 표현해야 한다.

여기서 $G$는 $\theta_g$를 파라미터로 갖는 MLP로 표현되는 미분 가능한 함수(differentiable function)이다.

또한 우리는 두 번째 MLP로 하나의 스칼라를 output으로 가지는 $D(x;\theta_d)$를 정의할 수 있다. $D(x$)는 $x$가 생성자의 데이터 $p_g$가 아닌 실제 데이터 분포에서 추출됐을 확률을 계산한다.

우리는 $D$가 최대한 입력받은 샘플에 대해 실제 데이터인지 $G$로부터 생성된 데이터인지 구별하여 라벨링을 정확하게 할 확률을 최대화하도록 훈련을 진행한다. 동시에 $G$는 $log(1-D(G(z)))$를 최소화하도록 훈련한다.

2-1. Object function

판별자 $D$, 생성자 $G$를 통해서 학습해야 하는 목적함수는 위와 같다.

결국 $D$와 $G$는 value function $V(G, D)$를 놓고 2인 minmax game을 진행하는 것이다. $G$는 $V$를 최소화하고, $D$는 $V$를 최대화한다.

목적함수를 살펴보면,

• 판별자 $D$는 입력받은 데이터가 진짜 데이터 분포에서 나왔다고 판별할 경우 $D(x)=1$, $G$가 생성한 가짜 데이터로 판별할 경우 $D(x)=0$으로 출력한다. D는 입력받은 데이터를 올바르게 분류하도록 학습하여야 하기 때문에 목적함수 $V(D, G)$의 각 항의 값이 $0$이 되도록 만들어야 하고, $V(D, G)$를 최대화하는 값은 0이 된다.
• 생성자 $G$는 $G$가 생성한 데이터에 대해 $D$가 실제 데이터 분포에서 나온 것으로 판단하게 만들어야 하기 때문에 $D(G(z))=1$이 되도록 학습해야 한다. 결과적으로 목적함수 $V(D, G)$의 값이 음의 무한대($log(0)$)로 발산하도록 만들어야 한다.

적대적 신경망의 반복 학습을 진행할 때 $D$를 최적화하는 것은 계산상 불가능에 가깝고, 한정된 데이터셋으로 반복 학습을 진행함에 따라 신경망의 과대적합이 발생할 수 있다.

따라서, 우리는 $D$의 가중치 계산을 줄이기 위해 $k$번의 스텝으로 $D$의 학습을 진행하는 동안 $1$번의 스텝으로 $G$의 학습을 진행하는 방법을 택한다. 이를 통해 $D$는 최적의 성능에 가깝게 유지가 되고 $G$ 또한 충분히 느린 속도로 변화한다.

학습 루프의 스텝 초반에 $G$의 성능이 저조할 떄, 원본 학습 데이터와 $G$가 만들어낸 학습 데이터 간의 차이가 크게 발생하므로 $D$는 높은 확률로 판별에 성공할 것이다. 따라서 학습 초기에 목적함수의 $log(1-D(G(z)))$는 0에 수렴한다.

이런 경우 $G$는 $log(1-D(G(z)))$를 최소화하는 대신 $log(D(G(Z)))$를 최대화하는 방향으로 학습을 진행할 수 있다. 이렇게 목적함수를 설정함으로써 학습 초기에도 $G$와 $D$의 그레디언트를 더욱 강력하게 만들 수 있다.

3. Theoretical Results

생성자 $G$는 $z\sim p_z$를 따르는 분포에서 얻은 표본인 $G(z)$를 확률 분포 $p_g$로 암묵적으로 정의한다. 결국 우리는 충분한 학습을 통해 Algorithm 1이 $p_{data}$에 대한 좋은 예측기로 수렴하기를 원한다.

이번 섹션의 학습은 모집단의 분포가 정해지지 않은 비모수적(non-parametric)으로 수행되어 결과를 산출한다. 확률 밀도 함수 공간상에서의 수렴을 통해 모델의 성능이 무한함을 보여줄 것이다.

섹션 3.1에서는 목적함수의 minmax game이 전역 최적점(global optimum)을 갖는 것($p_g = p_{data}$)을 보여줄 것이다. 그리고 섹션 3.1에서는 Algorithm 1이 목적함수(Eq 1)를 최적화하여 우리가 원하는 결과를 얻는다는 것을 보여줄 것이다.

Algorithm 1

GAN의 mini batch를 이용한 SGD(Stochastic Gradient Descent) 알고리즘이다.

$D$(Discriminator)의 학습 :

1. noise 분포 $p_g(z)$를 이용하여 noise를 첨가한 $m$개의 mini-batch 데이터 {$z^{(1)}, … , z^{(m)}$}을 만든다.
2. $D$는 $G$로부터 생성된 데이터 분포 $p_{data}(x)$에서 샘플링한 mini-batch 데이터 {$x^{(1)}, … , x^{(m)}$}을 평가한다.
3. 확률적인 경사 상승(ascending its stochastic gradient)을 통하여 $D$의 가중치를 업데이트한다.

$G$(Generator)의 학습($D$가 $k$번의 학습을 진행한 이후 학습 진행) :

1. noise 분포 $p_g(z)$를 이용하여 noise를 첨가한 $m$개의 mini-batch 데이터 {$z^{(1)}, … , z^{(m)}$}을 만든다.
2. 확률적인 경사 상승(decsencding its stochastic gradient)을 통하여 $G$의 가중치를 업데이트한다.

gradient에 기반을 둔 업데이트는 어떤 gradient-based learning rule을 쓰더라도 무방하다. 본 논문에서는 momentum 알고리즘을 사용했다.

3.1 Global Optimality of $p_g = p_{data}$

우리는 첫번째로 생성자 $G$에 대한 최적의 판별자 $D$를 고려해야 한다.

Proposition 1.

고정된 $G$에 대하여 최적의 판별자 $D$는 식 (2)와 같다.

Proof.

임의의 생성자 $G$가 주어졌을 때, 그에 대한 판별자 $D$의 학습 기준은 식 3의 $V(G, D)$의 수치를 최대화하는 것이다.

실수 집합에서 $(0, 0)$을 제외한 모든 $(a, b)$의 조합에서 $y -> alog(y) + blog(1-y)$는 닫힌 구간 $[0, 1]$에서 $y = \frac a {a+b}$일 때 최대값을 갖는다.

판별자 $D$는 지지집합의 합집합인 $Supp(p_{data}) \cup Supp(p_g)$ 외부에서 정의될 필요가 없다.

$Y$가 입력 데이터 $x$에 대해 $x = p_{data}$일 경우 $y=1$, $x = p_g$일 경우 $y=0$을 산출할 때, $D$의 학습 목적은 $P(Y=y|x)$에 대한 log-likelihood를 최대화하는 것임을 주목해보자. Eq 1에서의 minmax game은 다음과 같이 재구성될 수 있다.

Theorem 1.

가상의 학습 기준 $C(G)$는 전역 최저점에 $p_g = p_{data}$일 때만 도달한다(필요충분조건). 이 때, $C(G)$는 $-log(4)$의 값을 갖는다.

Proof.

Eq (2)에 따라 $p_g = p_{data}$이면 $D^*_G(x) = \frac 1 2$이다. 이를 Eq (4)에 적용하면, 우리는 $C(G) = log\frac 1 2 + log\frac 1 2 = -log4$임을 알 수 있다.

목적함수는 $-log4$임을 관찰하여, 우리는 $p_g=p_{data}$인 경우만을 고려하여 $C(G) = V(D^*_G, G)$의 등식에서 손실함수의 식을 뺄셈하면 다음과 같은 식을 얻는다.

여기서 KL은 두 확률분포의 차이를 Entropy(불확실도)를 이용하여 계산하는 함수인 Kullback-Leibler divergence(KLD)이다. 우리는 Eq (5)에서 데이터 생성 프로세스와 모델의 분포 간의 관계를 Jensen-Shannon divergence(JSD)를 이용하여 표현할 수 있는 것을 발견하였다.

JSD는 KLD가 두 분포 사이의 차이를 거리로 나타낼 수 없다는 문제를 해결하기 위해 KLD의 두 분포 사이 평균을 구하는 하여 거리로 나타내는 방법이다.

두 분포 사이의 JSD는 항상 non-negative이고(거리이기 때문에) 두 분포가 동일한 경우에만 0의 값을 갖기 때문에, 우리는 $C^* = -log(4)$인 경우가 $C(G)$의 전역 최적점이며 그 해는 $p_g = p_{data}$인 경우밖에 없다는 것을 증명할 수 있다.

위의 증명 과정을 통해, 생성 모델은 원본 데이터 생성 프로세스를 완벽하게 따라할 수 있다는것이 증명되었다.

3.2 Convergence of Algorithm 1

Proposition 2.

• $G$와 $D$가 충분한 성능을 갖고
• Algorithm 1에서 판별자 $D$가 주어진 생성자 $G$에 대한 최적점에 도달하는 것이 가능하며
• $p_g$가 Eq 1의 목적함수를 향상시키는 방향으로 업데이트된다면,

$p_g$는 $p_{data}$로 수렴한다.

→ G가 생성한 이미지의 분포가 현실 데이터의 분포로 수렴한다.

Proof.

상기된 기준에 따라 목적 함수 $V(G, D)$를 $p_g$를 파라미터로 갖는 함수 $U(p_g, D)$로 표현한다. 여기서 $U(p_g, D)$는 $p_g$에 대한 컨벡스(convex) 함수임에 주목하자.

컨벡스 함수의 위에 있는 하방 도함수(subderivatives)는 원시함수의 전역 최대점에서의 도함수를 포함한다. 다시말해서, 만약 $f(x)=\sup_{\alpha\in A}f_{\alpha}(x)$ 와 $f_{\alpha}(x)$가 모든 $\alpha$에 대해 도메인 $x$에서 컨벡스일 때, $\beta = \arg\sup_{\alpha \in A}f_{\alpha}(x)$임을 만족할 경우 $\partial f_{\beta}(x) \in \partial f$ 인 것을 알 수 있다.

이 과정은 주어진 $G$와 그에 대응하는 최적의 $D$에 대해 경사 하강을 진행하여 계산하는 것과 동치이다.

Theorem 1에서 증명된 것과 같이, $\sup_D U(p_g, D)$ 는 유일한 전역 최적점을 갖는 컨벡스이고, 따라서 $p_g$에 대한 충분히 작은 업데이트를 통해서 $p_g$는 $p_x$에 수렴할 수 있다. 증명을 완료한다.

현실의 문제에서 에서 적대적 신경망은 생성 함수 $G(z;\theta_g)$를 통해 제한적인 $p_g$의 분포를 표현하고, 우리는 $p_g$대신 $\theta_g$를 최적화한다. G를 구성하기 위해 MLP를 사용하는 것은 parameter space의 여러 가지의 중요점들을 내포할 수 있다.

그러나, 현실의 문제에서 MLP를 사용함으로써 우수한 성능을 내는 것은 모델에 대한 이론적인 보증이 부족함에도 불구하고 해당 모델이 합리적으로 쓸 만한 모델이라는 것을 알 수 있다.

4. Advantages and disadvantages

이러한 새로운 프레임워크는 이전에 존재했던 모델링 프레임워크와 비교하여 advantage와 disadvantage가 존재한다.

Disadvantage

• $p_g(x)$의 명시적인 표현이 존재하지 않는다.
• 학습을 진행하는 동안 $D$는 $G$와의 동기화를 계속 유지하여야 한다. ($D$의 업데이트가 진행되지 않으면 $G$도 학습을 진행하다 업데이트를 멈추게 된다.)

Advantage

• 더이상 Markov chain이 학습 과정에서 필요하지 않고, 오직 gradient를 얻기 위한 역전파만이 필요하다.
• 학습을 진행하는 동안 추론(inference)가 필요하지 않다.
• 모델에 다양한 function이 통합되어 사용될 수 있다.

위의 세 개의 장점은 계산적인 관점에서 바라본 장점이다. 적대적 신경망의 생성자는 데이터의 샘플을 통해 바로 업데이트되지 않고, 단지 판별자의 gradient를 조정함으로써 통계적인(statistical) 이득을 얻을 수 있다. 이 말은 결국 인풋 데이터의 항목들이 $G$의 parameter로 바로 복사되지 않는다는 뜻이다.

적대적 신경망의 또 다른 장점은, 신경망이 아무리 sharp하고 퇴화된(degenerate) 분포라도 학습하여 표현할 수 있다는 것이다. 마르코프 체인은 이와 같은 경우에 더 흐릿한 분포가 필요하다.

5. Conclusions and future work

생성적 적대 신경망은 다음과 같은 여러 확장판을 포함한다.

1. 생성자 $G$와 판별자 $D$의 input에 $c$를 더하여 조건적 생성 모델 $p(x|c)$를 만들 수 있다.
2. 보조적인 신경망(auxiliary network)을 훈련시킴으로써 주어진 $x$를 이용해 $z$에 대한 예측을 만들어 학습된 근사 추론(learned approximate inference)을 수행할 수 있다. 이 과정은 wake-sleep 알고리즘을 통해 추론 신경망을 훈련시키는 과정과 비슷하다. 하지만 생성적 신경망에서는 훈련을 완료한 고정된 생성자 $G$에 대해 추론 신경망이 학습할 수 있다는 장점이 있다.
3. $x$의 지수의 부분 집합인 $S$에 대하여 모든 조건부 집합인 $p(x_s | x_{\not S})$를 근사적으로 모델링할 수 있다. 적대적 신경망을 통하여 MP-DBM(Multi Prediction-Deep Boltzman Machine)의 확률적 확장을 구현할 수 있다.
4. 준지도학습(semi-supervised learning) : 부분적으로 라벨링된 데이터에 대하여 판별자 혹은 추론 신경망의 feature를 이용하여 분류기의 성능을 향상시킬 수 있다.
5. 효율성 증진 : 훈련 중에 생성자 $G$와 판별자 $D$를 조정하거나 샘플 $z$의 더 나은 분포를 사용하는 방법 중 부분적으로 더 나은 방법을 택하여 훈련의 속도를 대폭 가속화할 수 있다.

6. How to evaluate GANs?

생성 모델(Generative model)이 생성한 이미지는 원본 이미지가 존재하지 않으므로, ground truth가 없다. 따라서 GAN이 발표된 이후 후속 연구에서 GAN 모델을 평가하기 위한 평가지표가 활발히 연구되고 있다.

앞서 GAN의 논문 리뷰에서 살펴보았듯이, 생성 모델의 목표는 최대한 실제 이미지 데이터의 분포를 근사하여 실제에 가까운 이미지를 생성하는 것이다. 이러한 목표에 대한 달성도를 평가하기 위해 여러 metric(측도)이 제시되었다.

이어서 모델을 평가하기 위한 측정 방식에 따른 분류를 통해 GAN 모델 측정 방법을 설명하겠다.

6-1. Qualitative GAN Generator Evaluation(정성적 생성모델 평가)

6-1-1. Rating and Preference Judgement

가장 많이 사용되는 정성적 모델 평가 방법으로, 인간 심판이 직접 육안으로 생성된 이미지와 실제 이미지 간의 비교를 통해 적절도(fidelity)를 평가하여 순위나 등급을 매기는 방법이다.

그러나 육안으로 평가시 평가하는 사람에 따라 지표가 나누어지기 때문에 주관적이라는 단점이 있고, 평가하는 사람의 도메인 지식의 영향이 크기 때문에 적용할 수 있는 분야가 한정적이라는 단점이 있다.

6-1-2. Rapid Scene Categorization

Rapid Scene Categorization 방법은 이미지를 보고 평가하는 시간을 매우 짧게 제한하여(100ms) 이 짧은 시간 동안 인간 심판이 육안으로 이미지가 원본 데이터인지 생성 모델이 생성한 가짜 데이터인지 구별하도록 한다.

이 방법 또한 인간의 육안으로 평가를 진행하기 때문에 6-1-1에서의 단점과 같은 단점이 존재한다.

6-1-3. 1-Nearest Neighbor Classifier (1NNC)

1-Nearest Neighbor Classifier(1NNC)는 생성된 데이터와 실제 데이터를 구분하는 성능을 측정하여 GAN 생성 모델의 성능을 평가하는 방법이다.

1NNC는 생성된 데이터와 실제 데이터를 각각 2n개씩 묶어서 1-NN Classifier를 훈련시킨다. 1-NN Classifier는 각 데이터 포인트와 가장 가가운 이웃을 기반으로 데이터 포인트의 클래스를 예측한다.

1NNC의 성능은 Leave-One-Out(LOO) accuracy로 측정된다. LOO accuracy는 1-NN Classifier가 각 데이터 포인트에 대한 클래스를 올바르게 예측하는 비율에 대한 정확도이다.

1NNC의 LOO accuracy가 높을수록, GAN 생성모델이 원본 데이터 분포를 잘 학습했다는 것을 의미한다.

1NNC는 GAN 모델을 평가하는 데 유용한 지표이지만, 데이터 분포가 매우 복잡한 경우 정확하게 계산하기 어렵다는 단점과 1-NN Classifier가 데이터의 특성에 따라 편향될 수 있다는 단점이 존재한다.

6-2. Quantitative GAN Generator Evaluation(수치적 생성모델 평가)

6-2-1. Average Log-likelihood

앞서 리뷰한 이안 굿펠로의 GAN 논문의 Experiment에서는 이미지의 품질을 평가하기 위해 Average Log-likelihood를 사용했다. Average Log-likelihood는 생성 모델이 원본 이미지의 데이터 분포를 얼마나 잘 학습하였는지를 나타낸다. 이 값이 높을수록 생성 모델이 원본 이미지 데이터 분포를 잘 학습하였다는 것이다.

Average Log-likelihood는 GAN 모델을 평가하는 데 유용한 지표이지만, 계산하려는 데이터의 분포가 정규 분포를 따르는 경우에만 정확하게 계산할 수 있다는 단점이 있다.

6-2-2. CID(Creativity, Inheritance, Diversity) index

CID index는 생성 모델이 생성한 데이터와 실제 데이터의 유사도를 측정하여 GAN 모델의 성능을 측정하는 방법이다. 이는 생성된 데이터가 얼마나 현실적인지, 또는 얼마나 원본 데이터의 분포와 유사한지를 나타낸다.

CID index는 세 가지의 평가지표를 곱한 지표이다.

Creativity : 실제 Image와 중복이 있으면 안 됨

Inheritance : 생성된 Image는 같은 스타일을 가져야 함 (생성된 image의 분포는 실제 image의 분포에 가까움.)

Diversity : 생성된 Image들은 서로 달라야 됨

6-2-3. Inception Score (IS)

Inception Score(IS)는 2016년 “Improved Techniques for Training GANs”라는 논문에서 Salimans et al.에 의해 처음 발표되었다. 논문 발표 이후 IS는 GAN을 평가하는데 있어 널리 사용된다.

IS는 1,000개의 class와 120만 개의 이미지로 구성된 ImageNet data를 이용하여 CNN을 기반으로 사전 훈련된(pre-trained) inception model을 이용하여 생성 모델이 생성한 이미지를 평가한다.

Inception model이 생성 모델이 생성한 이미지를 평가하는 기준에 있어서 중요하게 평가되는 두 가지의 지표가 있다.

1. Sharpness (S) = Quality (Q) = Fidelity (F) : 이미지의 품질

   생성된 이미지 데이터가 얼마나 원본 데이터와 유사한가

2. Diversity (D) : 이미지의 다양성

   생성된 이미지 데이터 간의 차이가 얼마나 존재하는가

위의 두 기준이 모두 부합하다면 IS는 높아진다. 둘 중 하나 또는 둘 다 거짓이라면 IS는 낮아진다.

6-2-4. Frechet Inception Distance (FID)

우선 Frechet Inception Distance(FID)는 IS와 동일하게 사전 훈련된 inception model을 통해 측정한다. FID는 생성 모델이 생성한 이미지의 퀄리티 일관성이 얼마나 유지되는지를 평가하는 데 사용하는 지표이다. 생성모델에서 만들어낸 생성 데이터를 실제 데이터와 생성된 데이터에서 얻은 feature의 평균과 공분산을 비교하여 생성 모델을 평가한다. 즉, 만들어진 이미지의 feature와 실제 이미지에 대한 feature가 비슷하다면 좋은 모델이라고 평가하는 것이다. FID 값이 낮을수록 실제 이미지와 생성된 이미지의 유사도가 높은 것을 뜻하며, 이미지의 퀄리티가 좋아짐을 뜻한다.

FID는 데이터의 평균 및 공분산을 통하여 성능을 측정하므로, 주어진 데이터의 특성에 따라 FID의 값이 크게 달라질 수 있다는 단점이 존재한다. 또한, 데이터의 분포가 매우 복잡한 경우 FID의 값이 정확하게 계산되지 않을 수 있다.

6-2-5. Kernel Inception Distance (KID)

Kerner Inception Distance(KID)는 FID와 상당히 비슷한 측정 방법으로 먼저 원본 데이터 셋에서 가능한 모든 조합으로 이미지 데이터 두 장을 뽑아 두 데이터 간의 차이를 구한다.

이 과정을 반복하여 모든 조합에서의 차이를 더하고 조합 수 만큼 나누어 이미지 데이터의 차이의 평균을 구한다. 마찬가지로 생성된 데이터 셋에서 도 두 이미지 데이터 간의 차이의 평균을 구한다.

마지막으로 하나는 원본 데이터셋에서, 다른 하나는 생성된 데이터셋에서 이미지를 뽑아서 두 데이터 간의 차이의 평균을 구한다.

위 과정을 통해 구한 세 개의 평균값을 이용하여 KID 값을 구한다.