앙상블 정리
앙상블 정리
0. 단일 모델의 한계
결정 트리는 이해하고 해석하기 쉬우며, 사용하기 편하고, 여러 용도로 사용할 수 있으며, 성능도 뛰어나다.
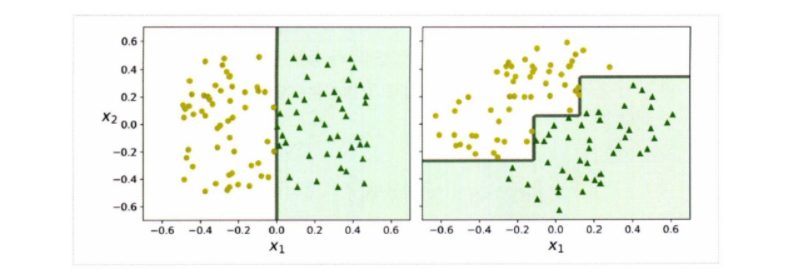
이런 결정 트리는 데이터의 축에 수직으로 분할하는 것을 기반으로 학습을 진행하기 때문에 항상 계단 모양의 결정 경계를 생성한다.
수직으로 분할한다는 특성 상, 결정 트리의 훈련 세트의 회전이 진행되면 결정 트리의 결정 경계가 불필요하게 구불구불해지는 것을 알 수 있다. 이런 한계를 극복하기 위해선 훈련 데이터의 축의 갯수를 축소시키고 데이터를 축의 방향으로 회전시키는 PCA 기법을 이용할 수 있다.
결정 트리를 비롯해 개별적인 머신러닝 모델은 각 모델의 한계 상 데이터의 변화에 따라 모델의 성능이 급격하게 떨어질 수 있다. 형식을 불문한 데이터에 항상 강건(Robust)한 머신러닝 모델은 존재하지 않는다.
1. 편향(Bias)과 분산(Variance)
1-1. Bias-Variance Decomposition
우리한테 주어진 현실 세계의 데이터에는 항상 우리가 제어할 수 없는 잡음(noise), 즉 에러(error)가 존재한다.
가상의 $y$라는 모델이 입력 $x$에 대해 항상 같은 결과를 출력하는 $F^*(x)$와 평균이 0, 분산이 $σ$인 정규분포를 따르는 에러 $\epsilon$로 이루어져 있다고 가정해 보자.
여기서 $F^*(x)$는 우리가 학습하고자 하는 target function이고, 에러 $\epsilon$은 독립적이고 동일한 분포를 가진다.
$y$에 대해 학습하려는 모델을 $\hat{F}(x)$로 설정하고 데이터셋 $x_{D}$에 대한 $\hat{F}(x)$의 기댓값을 $\overline{F}(x)$라고 할 때, $\overline{F}(x) = E[\hat{F_{D}}(x)]$ 라는 수식을 만족한다.
$y$와 $\hat{F}(x)$에 대한 MSE(Mean Squared Error)를 측정하는 수식을 세우고 약간의 트릭을 사용해 본 수식을 분해하면 우리는 모델의 Bias(편향)와 Variance(분산), 그리고 자연발생적인 노이즈 즉 에러의 분산이 도출된다.
여기서 도출되는 Bias란 우리가 학습하여 추정한 모델의 평균적인 추정값과 학습 타겟인 $y$값과의 차이를 나타낸다. 학습 모델의 Bias 값이 작을 경우 반복적인 모델 학습을 통해 평균적으로 학습 타겟 값을 잘 찾을 수 있는 것을 의미하고, Bias 값이 클 경우 반복적으로 학습하여도 학습 타겟을 잘 찾을 가능성이 낮아지는 것이다. 모델을 train/test 데이터를 분할하여 학습할 경우 Bias 값이 크면 과소적합(Underfitting)할 가능성이 커진다.
Vairance는 학습을 통해 모델이 산출한 결과값이 결과의 평균 값에 비해 얼마나 퍼져 있는 지를 나타낸다. Variance의 값이 작을 경우 noise 값이 바뀌어도 학습 모델의 결과값이 크게 바뀌지 않지만, Variance의 값이 클 경우 학습 모델의 결과값의 변동이 큰 것을 의미한다. 일반적으로 자유도(Degrees of Freedom)가 높은 모델이 Variance 값이 클 확률이 높고, train 데이터에 과대적합(Overfitting)할 가능성이 커진다.
1-2. 편향-분산 트레이드오프(Bias-Variance Tradeoff)
모델이 학습해야 할 파라미터가 많아지면 표본 데이터의 변수의 개수가 많아지므로, 모델의 자유도가 높아진다. 우리는 이것을 모델이 복잡해진다고 표현할 수 있다.
앞서 설명했듯이 모델의 복잡도가 증가하여 자유도가 증가할 경우 모델의 분산이 커지고 과대적합할 가능성이 커진다.
반대로 모델의 복잡도가 낮아지면 모델의 분산이 작아지고, 편향이 증가한다. 따라서 모델의 과소적합 가능성이 커진다.
단일 머신러닝 모델은 편향이 커지면 분산이 작아지고, 분산이 커지면 편향이 작아지는 트레이드오프(Tradeoff)가 발생한다. 이 현상을 편향-분산 트레이드오프(Bias-Variance Tradeoff)라 부른다.
2. 앙상블
2-1. 앙상블 모델의 도입
편향-분산 트레이드오프의 발생으로 인해 단일 머신러닝 알고리즘은 편향이 높은 대신 분산이 낮거나 분산이 높은 대신 편향이 낮은 단점을 보이고 있다.
현명한 개인의 판단보다 무작위로 선택된 다중의 집단지성을 따르는 것이 더 낫다는 말이 있다. 이를 대중의 지혜(Wisdom of the crowd)라 부른다.
개별의 단일 모델이 산출한 예측을 수집하여 최종 예측을 만들어낼 경우, 단일 모델보다 더 좋은 학습 성능을 얻을 수 있다. 이러한 아이디어에서 출발한 머신러닝 모델을 앙상블(Ensemble) 모델이라 부른다.
2-2. 앙상블 모델의 목적
앞서 설명했듯 개별 단일 모델의 성능은 Bias만 높거나 Variance만 높은 경우가 많다. 앙상블을 하여 학습을 진행할 경우 주로 단일 모델들의 Bias를 줄이는 것에 목적을 두거나 Variance를 줄이는 것에 목적을 둔다.
개별 단일 모델의 성능이 랜덤 추측보다 조금 더 높은 성능을 내는 약한 학습기(weak learner)일지라도, 충분하게 많고 다양하다면 개별 모델을 병합한 앙상블 모델은 강한 학습기(strong learner)가 될 수 있다.
모델의 Variance를 줄이는 앙상블 모델은 Bagging 계열의 모델이 있고, Bias를 줄이는 앙상블 모델에는 Adaboost 계열의 모델이 있다.
2-3. 앙상블 모델 설계의 중요 포인트
- 충분한 다양성을 얻기 위해 개별적인 components(단일 학습 모델)을 어떻게 구성할 것인가? → 각기 다른 단일 모델의 퍼포먼스를 나쁘지 않게 유지하며 어떻게 조합하면 다른 모형을 만들어 낼 수 있을 것인가? :: 90% 이상의 중요성 내포.
- 각 단일 모델의 결괏값을 어떻게 결합하여 최종 결과를 나타낼 것인가?
3. Bagging & Pasting
앙상블 모델 중에는 각각의 단일 개별 모델의 결괏값을 취합하여 병렬적으로 처리하는 방식으로 최종 결과를 도출하는 투표 기반 모델이 있다. 여기서 데이터 셋을 어떻게 활용하냐에 따라 앙상블 모델의 방식이 크게 두 가지로 나뉜다. 각 모델에 주어진 훈련 데이터셋의 중복을 허용하여 개별 단일 모델의 학습을 진행하는 배깅(Bagging)이나 허용하지 않는 비복원추출로 개별 단일 모델의 학습을 진행하는 방법인 페이스팅(Pasting)이 있다.
3-1. Bagging
배깅(Bagging) 학습 방법은 Bootstrap Aggregrating의 준말이다. 즉 복원 추출을 허용한 샘플링을 집합하여 훈련 데이터의 다양성을 확보한 학습을 진행하는 것에 목적이 있다.
복원추출을 허용하여 전체 데이터셋에서 추출한 개별 모델의 학습 데이터 샘플을 bootstrap이라고 부른다.
데이터 샘플인 bootstrap의 수를 N, 각 데이터가 모든 bootstrap에서 뽑히지 않을 확률이 p라고 할 때, $p=(1-1/N)^N → \lim_{n \to \infty}(1-1/N)^N = e^{-1} = 0.368$ 임을 알 수 있다.
따라서 데이터 샘플의 수가 충분히 많다면, 데이터가 샘플에 속할 확률이 1/3, 속하지 않을 확률이 2/3인 것이다.
배깅의 방법으로 앙상블 모델 학습을 진행할 경우 배깅 모델의 복잡도는 낮아지게 된다. 복잡도가 낮아지면 결국 편향이 줄어들고, 분산이 커진다는 것을 의미한다.
배깅에서 Bootstrap을 통한 샘플링으로 학습시킨 개별 단일 모델의 결괏값을 집합하는 방법(Aggregating)은 대표적으로 직접 투표(hard voting), 간접 투표(soft voting), 스태킹(stacked generalizetion) 세 갈래로 나뉜다.
- 직접 투표(hard voting)
- 각 단일 모델의 예측을 모아서 가장 많이 선택된 클래스를 예측하는 방법
- 간접 투표(soft voting)
- 각 단일 모델이 클래스의 확률을 예측할 수 있으면 개별 모델의 예측을 평균 내어 확률이 가장 높은 클래스를 예측하는 방법
- 스태킹(stacked generalization)
- 각 단일 모델의 예측을 취합하는 모델을 훈련시킨다. 주로 k-fold 교차검증 데이터셋을 이용하여 각 단일 모델의 예측값에 가중치를 부여하여 최종적인 메타 데이터셋을 만들어 학습을 진행한다.
배깅 방법을 이용한 대표적인 앙상블 모델에는 랜덤 포레스트(Random Forest)가 있다. 랜덤 포레스트는 의사 결정 트리를 앙상블하여 학습을 진행하는 모델로, 데이터 샘플을 복원추출하고 데이터의 feature를 무작위로 선택하여 학습을 진행한다.
3-2. Pasting
페이스팅(Pasting) 학습 방법은 개별 단일 모델이 주어진 훈련 데이터셋에서 중복을 허용하지 않고 비복원추출을 하여 학습을 진행하는 방법이다.
페이스팅 학습 방법은 각 샘플 데이터가 겹치지 않으므로, 일반적으로 배깅 학습 방법보다 앙상블 모델의 편향이 작고 분산이 크다고 볼 수 있다.
하지만 표본 샘플링의 무작위성이 무시되므로 전반적으로 배깅 방식이 페이스팅 방식보다 좀 더 나은 모델을 생성한다.
4. Boosting
부스팅(Boosting)은 투표 기반 모델과 다르게 단일 개별 모델을 직렬적으로 이어붙여 만든 앙상블 모델이다.
개별의 약한 학습기(weak learner)를 여러 개 이어붙여 앞의 모델을 보완해나가며 강한 학습기(strong learner)로 만든다는 것에 부스팅의 목적이 있다.