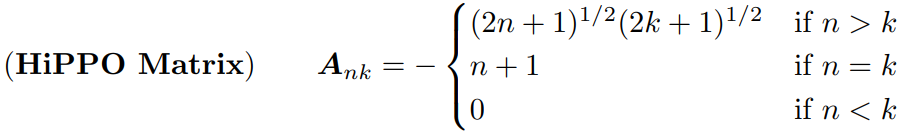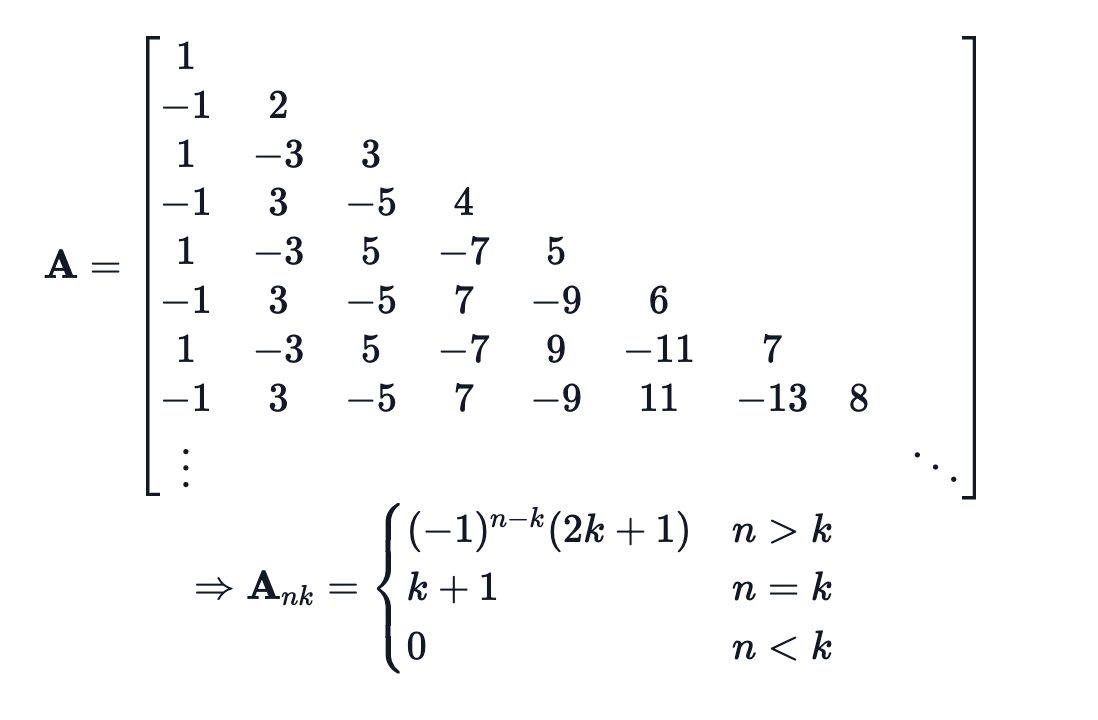Diffusion Models Without Attention & SSM(State Space Model) 완전 정복

Diffusion Models Without Attention 논문 리뷰

arxiv.org

0. Abstract

최근 고화질(hi-fidelity) 이미지 생성 분야의 발전 과정에서 Denoising Diffusion Probability Model(이하 DDPM)은 생성 모델로서 매우 중요한 Key player로 등장하게 되었다.

그러나 DDPM을 이용하여 고해상도 이미지를 생성하는 것에는 높은 Computational resource가 필요하다.

U-Net이나 Transformer 모델에서 이미지를 분할하여 input data로 이용하는 image의 패치화(patchifying)과 같은 방법을 이용해 이미지 처리 비용을 줄였지만, 이러한 방법은 원본 이미지의 표현 능력을 저하시키는 문제점이 존재한다.

위에서 언급한 단점을 해결하기 위해 본 논문에서는 Diffusion State Space Model(DiffuSSM)을 고안한다. DiffuSSM에서는 Attention mechanism을 대신해 State Space Model(상태 공간 모델)을 이용하여 좀 더 확장 가능한(scalable) Diffusion architecture를 구성하였다.

DiffuSSM architecture는 Diffusion process를 진행하면서, DDPM의 메소드인 이미지 전역 압축(global compression)에 의존하지 않으면서 이미지의 자세한 표현을 유지한다.

본 논문에서는 부동 소수점의 계산을 최적화하는 FLOP-eifficient architecture를 Diffusion에 적용하여 연구의 중요한 다음 스텝을 밟는 것을 의미하였다.

DiffuSSM은 ImageNet과 LSUN dataset에서의 광범위한 평가를 통해 기존의 Attention module을 이용하는 diffusion model과 비교하여 FID 및 Inception Score metric에서 동등하거나 우수한 성능을 보이며, FLOPS 사용량을 크게 줄이는 것을 보였다.

1. Introduction

Denoising Diffusion Probabilistic Model(DDPM)의 등장으로 인해 이미지 생성 분야에서 많은 발전이 일어났다.

DDPM은 latent variable(잠재 변수)의 denoising하는 과정을 반복적으로 진행한다. 반복적인 denoising을 충분하게 진행해줌으로써 고화질의 샘플을 생성할 수 있으며, 이런 기능을 통해 복잡한 시각적 분포를 포착할 수 있다는 장점이 있다.

그러나 DDPM을 더 높은 해상도로 확장하는 데에는 매우 큰 Computational challenge가 존재한다.

가장 큰 병목(bottleneck)으로는 고화질의 생성을 진행할 때 Self-attention에 의존한다는 점이 있다.

U-Net architecture의 경우, 이 병목 현상은 ResNet과 Attention layer를 결합하는 데에서 발생한다.

DDPM의 성능은 GAN(Generative Adversarial Networks)을 능가하지만, DDPM architecture는 Multi-head attention layer를 필요로 한다.

Transformer model의 구조에서 Attention mechanism은 모델의 중심 구성 요소임을 누구도 부정할 수 없을 것이고, 이미지 합성에서 이미지 합성의 SOTA를 달성하는 데 중요한 역할을 하고 있다.

Attention의 계산 복잡도는 input sequence (length of $n$)에 대해서 2차적(quadratic, $O(n^2)$)으로 증가 하며, 이는 고해상도의 이미지를 다룰 때 너무 많은 계산을 요구하게 된다.

이런 Computational cost로 인해, 차원을 압축하여 이미지 표현을 압축하는 Representation compression method가 등장하게 되었다.

고해상도 이미지를 처리하는 architecture는 일반적으로 Patchifying 또는 Multi-scale resolution을 이용하여 이미지 처리를 하도록 하였다.

Patchifying은 계산 비용을 줄이긴 하지만, 고주파 영역의 중요한 공간적 정보(critical high-frequency spatial information)와 구조적 무결성(structural integrity)을 저하시킨다.

Multi-scale resolution은 Attention layer에서의 계산 비용을 줄이긴 하지만, downsampling을 통해 공간적 디테일을 저하시킬 수 있고 upsampling을 적용할 때 artifact를 도입할 수 있다.

• Architecture of DiffuSSM

Attention-free architecture인 DiffuSSM은 고해상도의 이미지 작업에서 Attention 대신 다른 architecture를 사용함으로써 Computational cost를 줄인다.

DiffuSSM은 Diffusion process에서 Gated Space State Model(using S4D)을 backbone으로 이용한다.

이전 작업에서 SSM 기반의 sequence model이 general-purpose의 Neural sequence model보다 뛰어난 것을 증명해 왔다.

이후 서술되는 4.DiffuSSM에서 DiffuSSM의 architecture에 대해 자세히 설명하도록 하겠다.

2. Related Work

Diffusion Models

DDPM은 diffusion에 기반한 모델들에 엄청난 발전을 가져왔다. 이미지 생성 task에서 diffusion-based model 이전에는 GAN에 기반한 모델들이 선호되었다. diffusion과 score-based model들은 이미지 생성 task에서 엄청난 발전을 이루었다. DDPM에서의 눈부신 발전의 키 포인트에는 sampling method를 발전시킨 것과, Classification-free guidance 두 가지가 있다.

추가적으로, Song et al.은 DDIM(Denoising Diffusioin Implicit Model)을 제시함으로써 diffusion model의 sampling 과정을 더 빠르게 진행하도록 발전시켰다.

잠재 공간(Latent Space)의 모델링은 deep generation model에서의 또 다른 핵심 테크닉 중 하나이다. VAE(Variational Auto Encoder)는 encoder-decoder 구조를 통해 잠재 공간을 학습하는 선구적인 모델이다. 이 모델에서의 compression idea가 최근에 Stable Diffusion으로 불리는 LDM(Latent Diffusion Models)에서도 적용되고 있다.

Architectures for Diffusion Models

초기의 Diffusion model은 U-Net 스타일의 architecture를 활용하였다. 이어지는 후속 연구들은 Multi-Scale 해상도 수준에서 더 많은 Attention layer를 추가, Residual connection, Normalization 등의 기술을 이용하여 U-Net을 개선하였다.

그러나 U-Net은 Attention mechanism에서 계속 증가하는 Computational cost때문에 높은 해상도로 확장하는 데 어려움이 있다.

최근 ViT(Vision Transformer)라는 강력한 확장 속성과 장기 범위 모델링 능력을 고려하여 대체 Architecture로 등장하였다. 이는 Convolution inductive bias가 필요하지 않다는 것을 의미한다.

Diffusion Transformers는 굉장히 유망한 결과를 보였다. 또 다른 hybrid CNN-Transformer Architecture 또한 학습 안정성을 향상시키기 위해 제안되었다. 우리의 연구는 순차 모델의 탐색과 관련된 디자인을 하여 고품질의 이미지를 생성하는 것에 중점을 두며, 완전한 Attention-free architecture를 목표로 한다.

Efficient Long Range Sequence Architectures

기본적인 Transformer architecture는 input으로 주어진 sequence를 tokenize한 후 individual token들의 문맥적 관계를 이해하기 위해 Attention mechanism을 이용한다.

그러나 $N$개의 token이 주어졌을 때 Attention mechanism의 Computational cost는 quadratic($O(N^2)$)이므로, 매우 긴 sequence를 만날 경우 큰bottleneck을 접하게 된다.

이를 해결하기 위해 Self-attention을 $O(N^2)$ 이하의 Computational cost로 근사하기 위해 Attention-approximation method가 도입되었다.

예를 들어 Mega에선 지수 이동 평균(Exponential Moving Average)과 단순화된 Attention unit을 결합하여 Transformer의 기본 성능을 능가하는 모델을 만들었다.

연구자들은 전통적인 Transformer model을 넘어 긴 시퀀스(elongated sequences)를 처리하는 데 능숙한 대체 model들도 탐구하였다. 그 중에서 State Space Model에 기반한(SSM-based) model architecture는 LRA 및 Audio benchmark에서 현대의 SOTA method를 능가하는 성과를 보였다.

3. Preliminaries

3.1. Diffusion Models

DDPM (Denoising Diffusion Probabilistic Models) Architecture

DDPM(Denoising Diffusion Probabilictic Models)은 주어진 데이터 분포를 학습하고 새로운 샘플을 생성하는 생성모델이다. DDPM은 Noise 추가와 제거 과정을 통해 데이터를 생성한다.

DDPM이 이미지를 생성하는 주요 단계는 다음과 같다.

1. Forward Process

Forward Process에서는 데이터에 점진적으로 Gaussian Noise를 추가한다. 이 과정은 다음과 같은 수식으로 표현된다.

\[q(\mathbf{x}_t \| \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})\]

여기서:

• $\mathbf{x}_t$ : 시간 $t$에서의 데이터 상태
• $\beta_t$ : 시간 $t$에서의 Noise Scale
• $\mathcal{N}$ : Gaussian Distribution (=정규분포)

2. Reverse Process

Reverse Process에서는 Noise를 제거하여 원본 데이터를 복원한다. 이 과정은 다음과 같은 수식으로 표현된다.

\[p_\theta(\mathbf{x}_{t-1} \| \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu\theta(\mathbf{x}_t, t), \Sigma\theta(\mathbf{x}_t, t))\]

• $\mu_\theta$, $\Sigma_\theta$ : parameterize된 평균과 분산

3. Loss Function

모델 학습을 위해, 손실 함수는 다음과 같이 정의된다.

\[L = \mathbb{E}{q} \left[ \sum{t=1}^T \text{KL}(q(\mathbf{x}_{t-1} \| \mathbf{x}_t, \mathbf{x}_0) \parallel p\theta(\mathbf{x}_{t-1} \| \mathbf{x}_t)) \right]\]

• $\text{KL}$ : Kullback-Leibler Divergence
• $q$ : Forward Process 의 분포
• $p_\theta$ : Reverse Process 의 분포

요약

DDPM은 데이터에 점진적으로 Noise를 추가하고 이를 제거하는 과정으로 새로운 데이터를 생성한다. 이 과정은 순방향 과정(forward process)과 역방향 과정(reverse process)으로 구성되며, 모델은 KL-Divergence를 최소화하도록 학습된다. Noise 추가와 제거 과정은 Gaussian Distribution로 모델링되며, 각 단계는 시간에 따라 다른 Noise schedule을 가진다.

3.2 Architecture for Diffusion Models

Diffusion Models를 위한 아키텍처 부분에서는 데이터의 높이 $H$, 너비 $W$, 그리고 크기 $C$가 주어졌을 때, $\mu_{\theta}$를 parameterizing하는 방법에 대해 설명한다. 이 parameterizing은 $\mathbb{R}^{H \times W \times C} \rightarrow \mathbb{R}^{H \times W \times C}$ 의 mapping을 수행한다.

이미지를 생성하는 작업에서 원시 픽셀(raw pixels) 또는 사전 학습된 VAE Encoder에서 추출된 Latent Space Representation을 사용할 수 있다. 고해상도의 이미지를 생성할 때는 Latent Space에서도 $H$와 $W$가 크기 때문에, 이 함수가 처리 가능한 수준으로 만들기 위한 특수한 architecture가 필요하다.

U-Nets with Self-attention

U-Net architecture는 여러 해상도에서 합성곱과 하위 샘플링(sub-sampling)을 사용하여 고해상도 입력을 처리한다. 추가적으로, self-attention 레이어는 저해상도 블록에서 사용된다. 현재까지 self-attention을 사용하지 않고 최신 성능을 달성하는 U-Net 기반 diffusion 모델은 없다.

다음과 같이 표현할 수 있다.

1. $t_1, \ldots, t_T$는 image의 sub-sampling으로 생성된 낮은 해상도의 Feature map series다.
2. 각 스케일에서 ResNet이 적용된다: $\mathbb{R}^{H_t \times W_t \times C_t}$
3. 이러한 Feature map은 Upsampling되어 최종 출력으로 concat된다.
4. 이미지를 생성할 때 Self-attention layer는 flatten된 최저 해상도에서만 적용된다.
5. Feature map은 $H_t W_t$ vector의 sequence로 flatten된다.

Transformers with Patchification

Global contextualization에서 self-attention을 이용하는 것은 diffusion 모델에서 높은 성능을 달성하기 위해 중요하다. 따라서, 전체적으로 self-attention에 기반한 아키텍처를 고려하는 것이 자연스럽다.

Transformer 아키텍처는 self-attention을 사용하여 정보를 처리한다. 여기서 Trasformer를 이용하여 높은 해상도의 이미지를 처리하기 위해 patchification 방식을 사용한다:

1. 패치 크기 $P$가 주어졌을 때, Transformer는 이미지를 $P \times P$ 차원의 patch로 나눈다: $\mathbb{R}^{H/P \times W/P \times C’}$
2. 패치 크기 $P$는 이미지와 계산 수요의 유효한 granularity(세분성)에 직접적으로 영향을 미친다.
3. 이미지를 Transformer에 입력하기 위해, 이미지를 Flatten하고 임베딩 레이어를 통해 $(HW)/P^2$ hidden vector를 얻는다 : $\mathbb{R}^{(HW)/P^2}$
4. 큰 패치 크기는 공간적 세부 사항의 손실을 초래할 수 있지만, 계산 효율성을 제공한다.

4. DiffuSSM

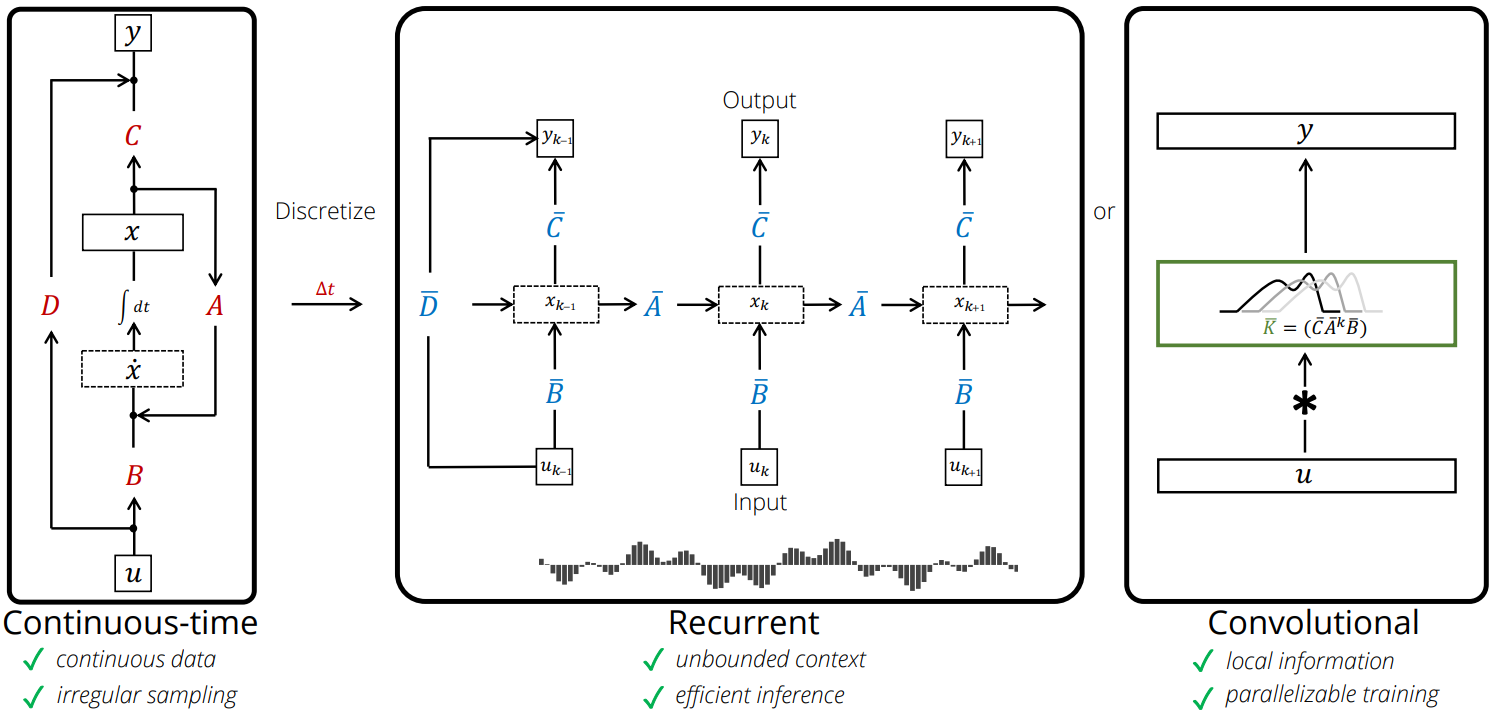
4.1. State Space Models (SSMs)

Definition of State Space Model

• 기초 개념
  • 물리학적 계(system)를 입력(input), 출력(output), 상태 변수(state variable)의 1차 상미분 방정식(1st-order ODE)으로 표현하는 수학적 모델. 기존에는 전기전자 공학 분야의 제어 이론에서 주로 사용되었다.

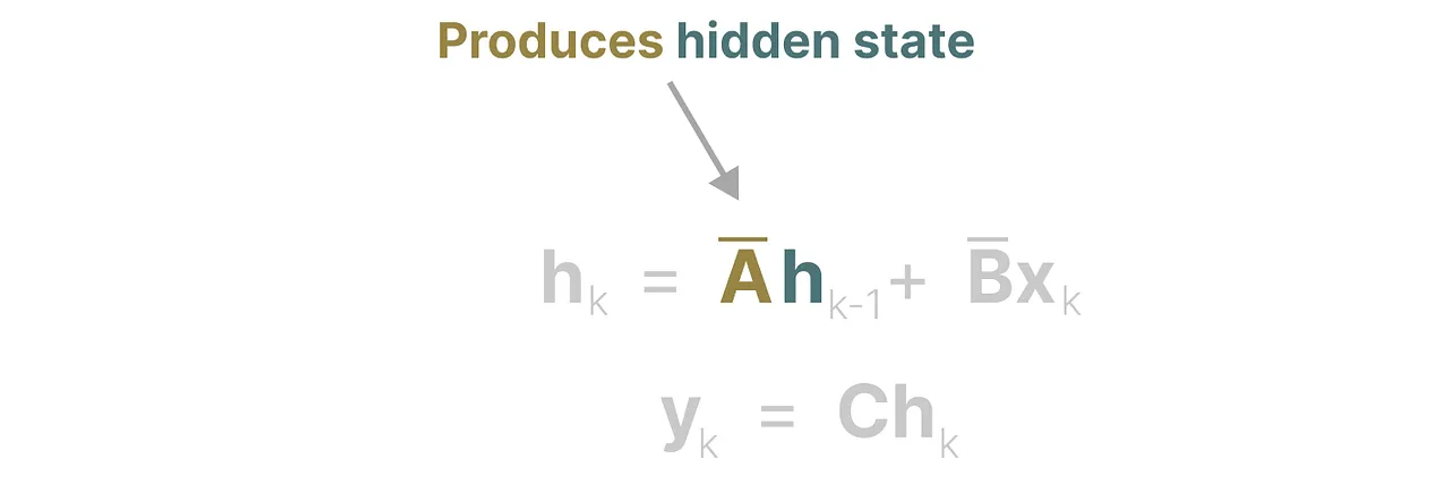
  • $h’(t) = Ah(t) + Bx(t)$ $h$ : hidden state, $x$ : input sentence

    $y(t) = Ch(t) + Dx(t)$ $y$ : output sentence, $A,B, C, D$ : (Learnable | Fixed) Parameter

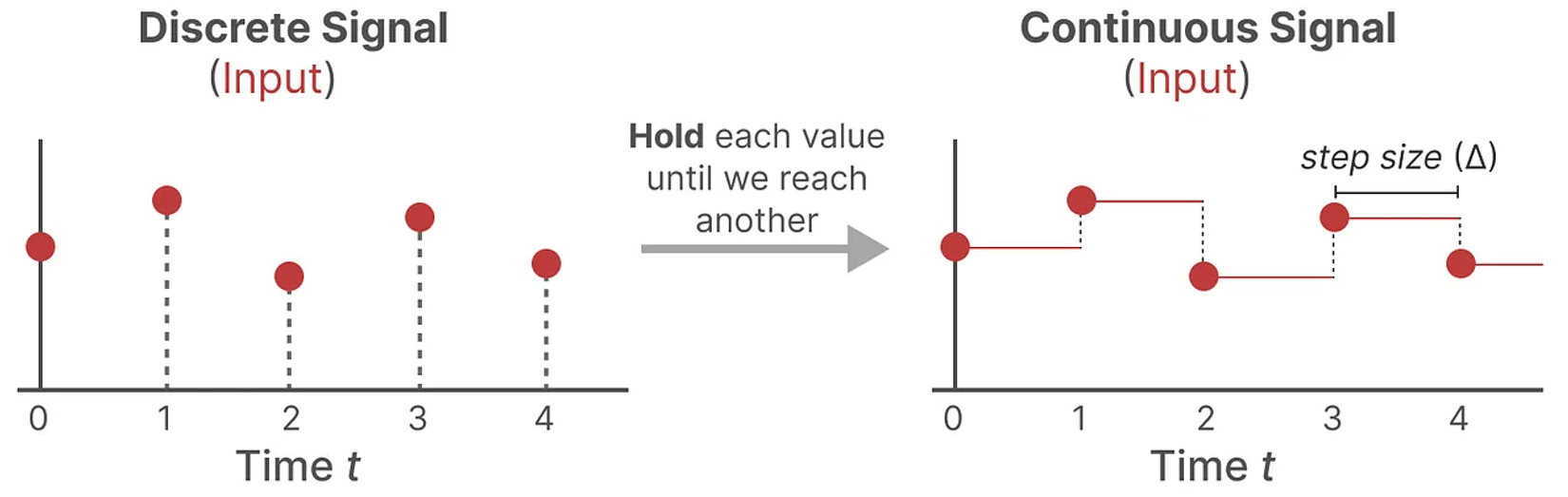
Continuous signal to Discrete signal

기존의 SSM은 input signal을 continuous sequence로 입력받게 설계되었지만, 우리가 컴퓨터로 signal을 계산하기 위해 continuous sequence를 discrete sequence로 변환해 주어야 한다.

Discretization의 방법에는 여러 가지(Zero-order hold, Bilinear transformation, Backward Euler method, etc…)가 있지만 그 중에서 Zero-order hold와 Bilinear transformation 두 가지를 설명하도록 하겠다.

• Zero-order hold, ZOH (영차 유지) → mamba에서 사용

이산 신호를 받을 때마다, 새로운 이산 신호를 받을 때까지 그 값을 유지한다.

→ 입력 신호 $u(t)$가 sampling 간격 동안 일정하다!

• SSM의 기본 아이디어가 일차 상미분 방정식임을 이용하면,

  • 이산 시간 SSM에서 sampling 주기 $T$ 후의 State vector $x[k+1]$를 계산하면 다음과 같다.

    (Zero-order hold에 따라 입력 $u(t)$가 주기 동안 일정하다고 가정)

    $x((k+1)T) = e^{A T} x(kT) + \int_{0}^{T} e^{A(T-\tau)} B u(kT) \, d\tau$

    $t = kT, t+T = (k+1)T$

    $A_d = e^{A T}$

    $B_d = \left( \int_{0}^{T} e^{A(T-\tau)} \, d\tau \right) B = A^{-1} (e^{A T} - I) B$

  로 parameter를 얻을 수 있다.

단, $A^{-1}$이 필요하다! → A matrix가 Invertible해야 한다!

• Bilinear transform (==Tustin’s method, 쌍선형 변환) → S4에서 사용

Input signal의 Continuous 시간 시스템의 Laplace domain(S-domain)을 Discrete 시간 시스템의 Z-domain으로 변환한다.

변환 공식

$s = \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}}$

• $s$ : 연속 시간 Laplace domain function
• $z$ : 이산 시간 Z-domain function
• $T$ : sampling 주기

Recursive view of an SSM - using Bilinear Transform

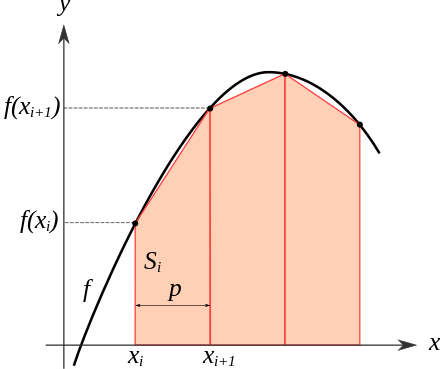
• Trapezoidal method

  

  Continuous signal을 discretize하기 위해, 연속함수의 적분 값을 근사하는 수치 적분(Numerical Integration)을 이용하여야 한다.

  함수 $f$가 구간 $[t_n, t_{n+1}]$에 정의된 대표 곡선 아래의 영역을 사다리꼴로 동화시키고 그 면적을 계산하는 원리를 사용하는 Trapezoidal method (사다리꼴 방법)을 이용할 수 있다.

  $\int_{a}^{b} f(x) \, dx \approx \frac{b - a}{2} \left[ f(a) + f(b) \right]$

  구간을 $n$개의 작은 구간으로 나누면:

  $\int_{a}^{b} f(x) \, dx \approx \frac{h}{2} \left[ f(x_0) + 2 \sum_{i=1}^{n-1} f(x_i) + f(x_n) \right]$

  $\therefore$ $T : T = (t_{n+1} - t_n) \frac{f(t_n) + f(t_{n+1})}{2}$

• Discretization (이산화 과정) - Bilinear transform

  Trapezoidal method를 이용해 SSM에서 다음과 같은 식을 얻을 수 있다. $x_{n+1} - x_n = \frac{1}{2} \Delta (f(t_n) + f(t_{n+1}))$

  여기서 $\Delta = t_{n+1} - t_n$ 이다.

  만약 $x’_n = A x_n + B u_n$ (SSM 수식의 첫 번째 줄)이 $f$에 해당한다고 하면, 다음과 같이 수식을 정리할 수 있다.

  $x_{n+1} = x_n + \frac{\Delta}{2} (A x_n + B u_n + A x_{n+1} + B u_{n+1})$

  이를 변형하면

  $x_{n+1} - \frac{\Delta}{2} A x_{n+1} = x_n + \frac{\Delta}{2} A x_n + \frac{\Delta}{2} B (u_{n+1} + u_n)$

  이고,

  한 번 더 위의 식을 정리하면

  $(I - \frac{\Delta}{2} A) x_{n+1} = (I + \frac{\Delta}{2} A) x_n + \frac{\Delta}{2} B (u_{n+1} + u_n)$ 으로 표현할 수 있다.

  따라서, 최종적으로 다음과 같은 형태가 된다.

  $x_{n+1} = (I - \frac{\Delta}{2} A)^{-1} (I + \frac{\Delta}{2} A) x_n + (I - \frac{\Delta}{2} A)^{-1} \frac{\Delta}{2} B (u_{n+1} + u_n)$

  여기서, ZOH를 적용하면 $u_{n+1} \approx u_n$ (제어 벡터는 작은 $\Delta$ 동안 일정하다고 가정).

이렇게 Bilinear transform을 이용한 Discretized SSM의 수식을 정리하였다.

이 모델을 완전히 명확하게 하기 위해, 수식을 다음과 같이 정의할 수 있다.

1. 이산화된 시스템 방정식:
   $x_{n+1} = x_n + \frac{\Delta}{2} (A x_n + B u_n + A x_{n+1} + B u_{n+1})$

   이를 재정렬하여 다음과 같이 표현할 수 있다.
   $x_{n+1} - \frac{\Delta}{2} A x_{n+1} = x_n + \frac{\Delta}{2} A x_n + \frac{\Delta}{2} B (u_{n+1} + u_n)$ \

   그리고 Discretized SSM의 식을 다음과 같이 단순화할 수 있다. \(\begin{aligned} x_{n+1} - x_n &= \frac{\Delta}{2} (A x_n + A x_{n+1} + B (u_{n+1} + u_n)) \\ (I - \frac{\Delta}{2} A) x_{n+1} &= (I + \frac{\Delta}{2} A) x_n + \Delta B u_{n+1} \\ x_{n+1} &= (I - \frac{\Delta}{2} A)^{-1} (I + \frac{\Delta}{2} A) x_n + (I - \frac{\Delta}{2} A)^{-1} \Delta B u_{n+1} \end{aligned}\)

   여기서 $u_{n+1} \approx u_n$이라고 가정한다 (제어 벡터는 작은 $\Delta$에 대해 상수로 가정).

2. Discretized parameter:

   $\bar{A} = (I - \frac{\Delta}{2} A)^{-1} (I + \frac{\Delta}{2} A)$
   $\bar{B} = (I - \frac{\Delta}{2} A)^{-1} \Delta B$
   $\bar{C} = C$

3. 이산화된 모델의 최종 형태:

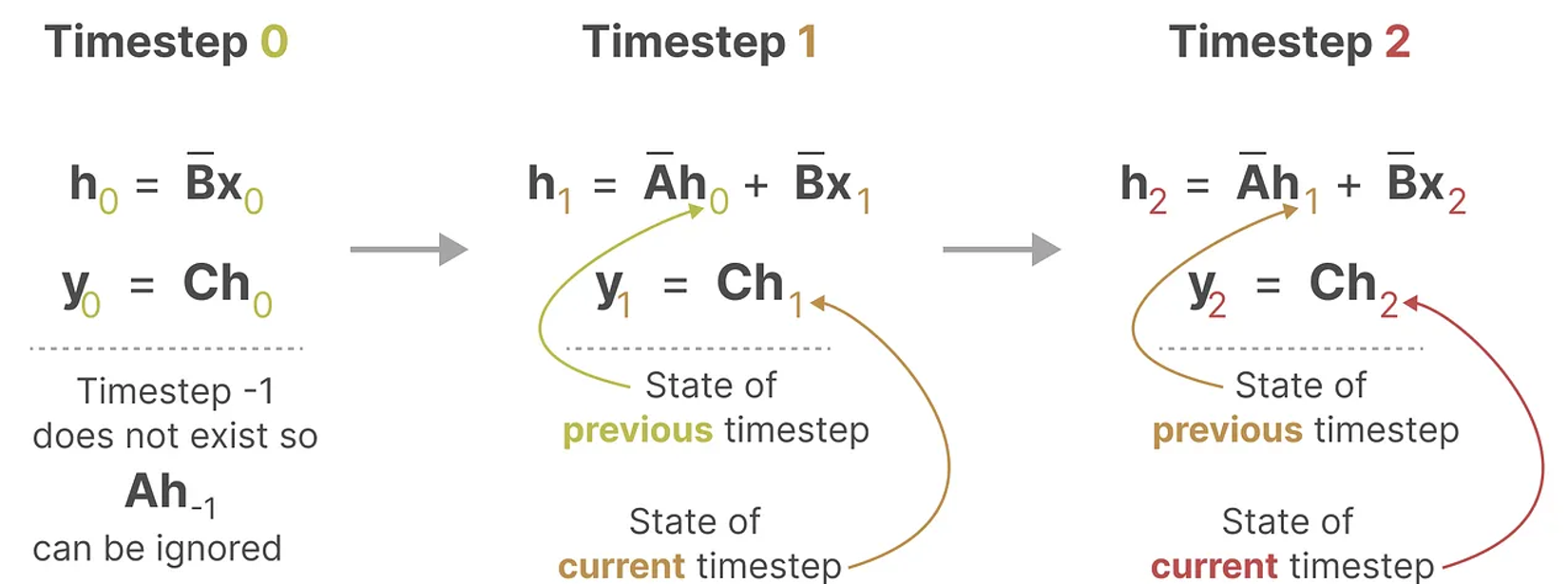
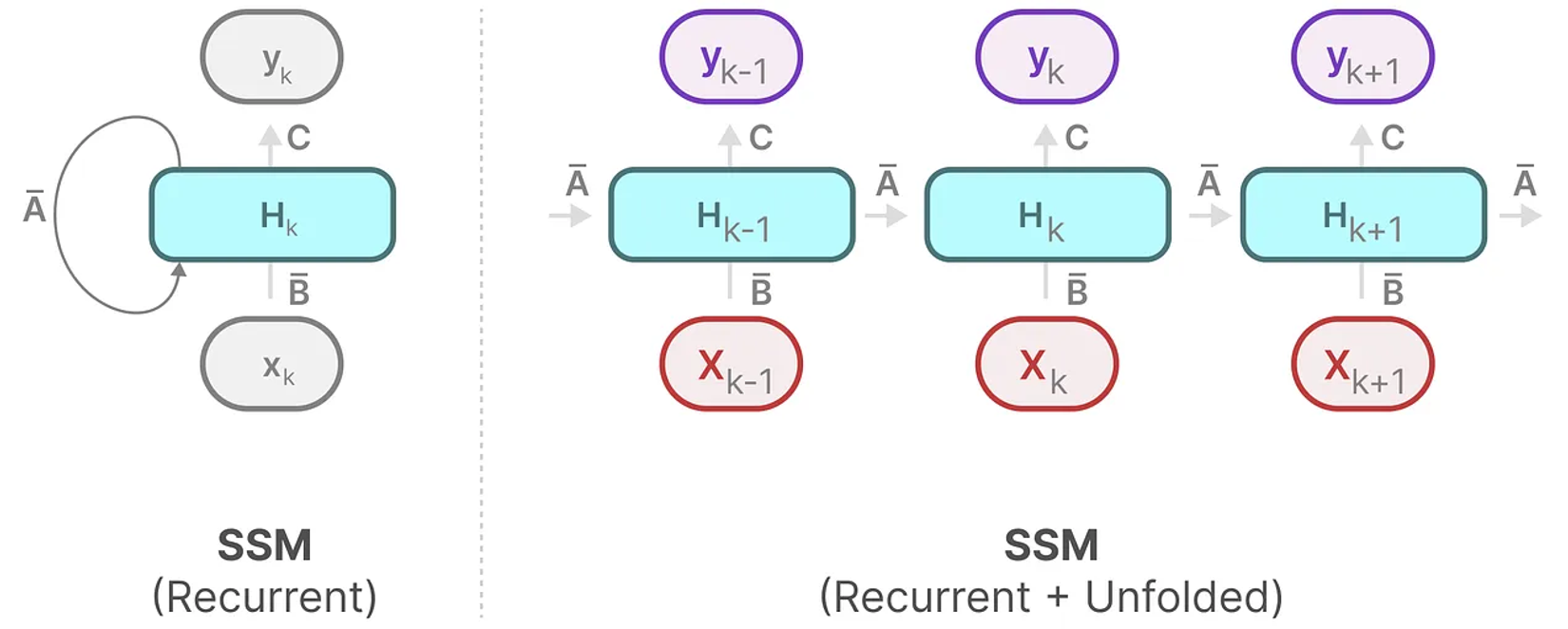
   $x_k = \bar{A} x_{k-1} + \bar{B} u_k$
   $y_k = \bar{C} x_k$

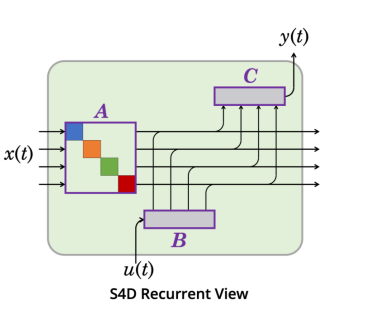
Recurrent Visualization

각 Timestep에서, SSM은 현재 입력이 이전 상태에 어떻게 영향을 미치는지 계산한 다음 예측된 출력을 계산한다.

이 계산 메커니즘은 RNN의 방식과 똑같이 표현될 수 있다.

Convolutive view of an SSM

앞서 설명한 SSM의 recurrence는 합성곱으로 작성할 수 있다. 이를 위해 SSM의 방정식을 반복한다.

$x_k = \bar{A} x_{k-1} + \bar{B} u_k$
$y_k = \bar{C} x_k$

• 시스템의 첫 번째 줄부터 시작하여 아래와 같이 표현할 수 있다.

  0단계 : $x_0 = \bar{B} u_0$

  1단계 : $x_1 = \bar{A} x_0 + \bar{B} u_1 = \bar{A} \bar{B} u_0 + \bar{B} u_1$

  2단계 : $x_2 = \bar{A} x_1 + \bar{B} u_2 = \bar{A} (\bar{A} \bar{B} u_0 + \bar{B} u_1) + \bar{B} u_2 = \bar{A}^2 \bar{B} u_0 + \bar{A} \bar{B} u_1 + \bar{B} u_2$

  $x_k$를 $(u_0, u_1, …, u_k)$로 parameterized function $f$로 작성할 수 있다.

• 이제 시스템의 두 번째 줄로 넘어가서, 방금 계산한 $x_k$값을 주입할 수 있다.

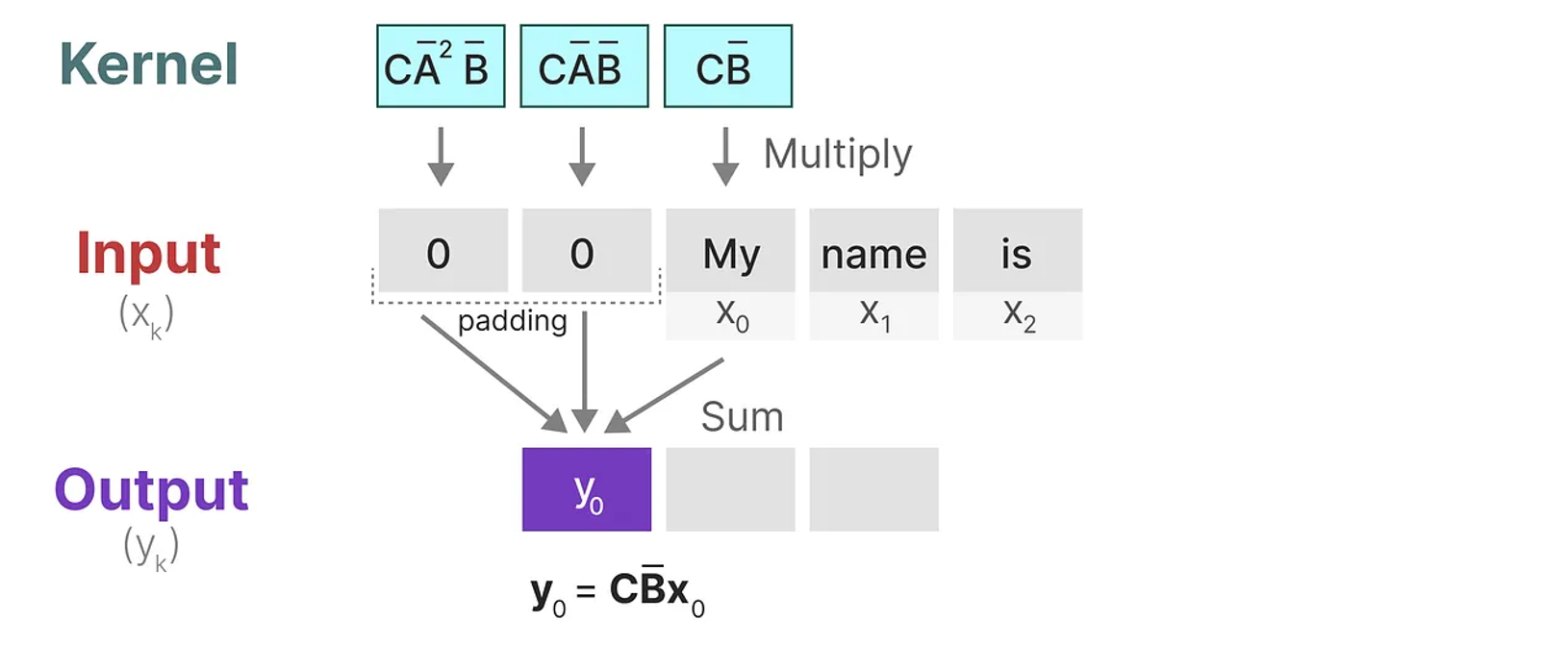
  0단계 : $y_0 = \bar{C} x_0 = \bar{C} \bar{B} u_0$

  1단계 : $y_1 = \bar{C} x_1 = \bar{C} (\bar{A} \bar{B} u_0 + \bar{B} u_1) = \bar{C} \bar{A} \bar{B} u_0 + \bar{C} \bar{B} u_1$

  2단계: $y_2 = \bar{C} x_2 = \bar{C} (\bar{A}^2 \bar{B} u_0 + \bar{A} \bar{B} u_1 + \bar{B} u_2) = \bar{C} \bar{A}^2 \bar{B} u_0 + \bar{C} \bar{A} \bar{B} u_1 + \bar{C} \bar{B} u_2$

각 단계의 계산에서 일정한 pattern이 보이므로, 이 규칙을 이용해 단계적인 전체의 계산을 한 번에 할 수 있지 않을까?

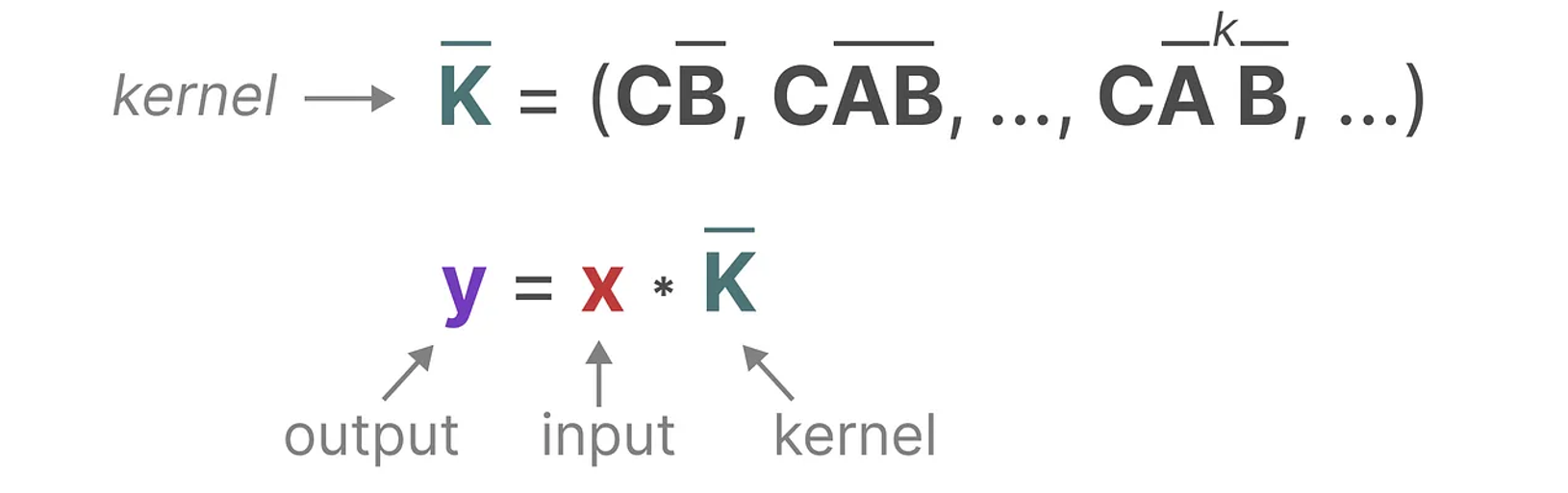
여기서, 합성곱 커널 $\bar{K}_k = (\bar{C} \bar{B}, \bar{C} \bar{A} \bar{B}, …, \bar{C} \bar{A}^{k} \bar{B})$ 을 $u_k$ 에 적용하여 $K * u$ 으로 표현할 수 있다.

행렬과 마찬가지로, 합성곱 커널이 이산화 과정 후 얻어진 것임을 명시하기 위해 $\bar{K}$ 에 bar를 표기하여 적용한다.

이는 논문에서 SSM 합성곱 커널(convolutive kernel)이라고 하며, 그 크기는 전체 input sequence와 동일하다.

이 합성곱 커널은 Fast Fourier Transform을 통해 계산 복잡도를 최적화하여 계산될 수 있다.

Fourier Transformation, Fast Fourier Transform(FFT)

• Fourier Series (푸리에 급수)
  • 정의

  주기적인 함수 𝑓(𝑡)를 주기 𝑇로 나타낼 때, 푸리에 급수는 이 함수를 삼각 함수의 합으로 표현하는 방법이다.

  • 수식

  주기 함수 𝑓(𝑡)f(t)는 다음과 같이 표현된다.

  $f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right) \right)$

  여기서 계수 $a_n$와 $b_n$는 다음과 같다.

  $a_0 = \frac{1}{T} \int_{0}^{T} f(t) \, dt$ $a_n = \frac{2}{T} \int_{0}^{T} f(t) \cos\left(\frac{2\pi nt}{T}\right) \, dt$

  $b_n = \frac{2}{T} \int_{0}^{T} f(t) \sin\left(\frac{2\pi nt}{T}\right) \, dt$

• Fourier Transformation (푸리에 변환)
  • 정의

  비주기적인 함수 𝑓(𝑡)를 주파수 영역에서 표현하는 방법으로, Fourier Transform (푸리에 변환, FT)을 사용한다. 이 변환은 시간 도메인에서 주파수 도메인으로 변환해주는 방법이다.

  • 수식

  Fourier Transform의 식은 다음과 같이 정의된다.

  $F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t}$$dt$

  이는 기본적으로 input signal인 f(t)가 연속적임(continuous)인 경우 정의된 것이다. 우리는 이산적인 경우를 관찰해야 하므로 Discrete Fourier Transform을 보아야 한다.

• Discrete Fourier Transform
  • 정의

  이산 신호를 주파수 영역으로 변환하기 위해 DFT(Discrete Fourier Transform)를 사용할 수 있다. 이는 푸리에 변환의 Discretized form이다.

  • 수식

  길이 𝑁인 이산 신호 𝑥[𝑛]에 대해 DFT의 식은 아래와 같이 정의된다.

  $X[k] = \sum_{n=0}^{N-1} x[n] e^{-i\frac{2\pi}{N}kn}$

  Input sequence를 $N$개로 나누어 $N$개의 token에 대해 각각 N번의 곱셈과 덧셈을 수행 → $O(N^2)$의 Time Complexity

  여기까지 보면 SSM과 Attention의 계산 복잡도가 같지만, 이 계산 복잡도를 줄일 수 있는 방법이 있다!

• Cooley-Tukey FFT Algorithm
  • 정의

  Cooley-Tukey FFT는 분할 정복(Divide-and-Conquer) 알고리즘을 사용하여 DFT를 효율적으로 계산한다. Cooley-Tukey FFT에서는 이를 위해 input signal을 recursive하게 절반씩 나누고, 각각에 대해 FFT를 계산한 후 이를 더해준다.

  • 수식
    1. Length of $N$인 discrete signal $x[n]$의 DFT는 아래와 같다.

    $X[k] = \sum_{n=0}^{N-1} x[n] e^{-i \frac{2\pi}{N} kn}$

  1. 입력 데이터의 분할 $x_{\text{even}}[m] = x[2m] \quad \text{for} \quad m = 0, 1, \ldots, \frac{N}{2}-1$ $x_{\text{odd}}[m] = x[2m+1] \quad \text{for} \quad m = 0, 1, \ldots, \frac{N}{2}-1$
  2. Even / Odd 부분에 대한 DFT의 계산 $X_{\text{even}}[k] = \sum_{m=0}^{\frac{N}{2}-1} x_{\text{even}}[m] e^{-i \frac{2\pi}{\frac{N}{2}} km}$ $X_{\text{odd}}[k] = \sum_{m=0}^{\frac{N}{2}-1} x_{\text{odd}}[m] e^{-i \frac{2\pi}{\frac{N}{2}} km}$

  3. 전체 DFT 계산 $X[k] = X_{\text{even}}[k] + W_N^k X_{\text{odd}}[k]$

     $X[k + N/2] = X_{\text{even}}[k] - W_N^k X_{\text{odd}}[k]$

     • 여기서 $W_N = e^{-i \frac{2\pi}{N}}$

• Time Complexity of Cookey-Tukey FFT Algorithm

  Cooley-Tukey FFT의 시간 복잡도는 다음과 같은 재귀 관계로 나타낼 수 있다.

  $T(N) = 2T\left(\frac{N}{2}\right) + O(N)$

  여기서 $2T\left(\frac{N}{2}\right)$ 는 두 개의 하위 문제(길이가 $N/2$ 인 부분 신호)에 대해 FFT를 계산하는 데 소요되는 시간이고, $O(N)$ 은 결과를 결합하는 데 필요한 시간이다.

다음은 Cooley-Tukey의 FFT algorithm을 재귀적으로 계산하여 Time Complexity를 증명하는 과정이다.

\[\begin{align*} T(N) &= 2T\left(\frac{N}{2}\right) + O(N) \\ &=2 \left[ 2T\left(\frac{N}{4}\right) + O\left(\frac{N}{2}\right) \right] + O(N) \\ &=4T\left(\frac{N}{4}\right) + 2O\left(\frac{N}{2}\right) + O(N) \\ &=4 \left[ 2T\left(\frac{N}{8}\right) + O\left(\frac{N}{4}\right) \right] + 2O\left(\frac{N}{2}\right) + O(N) \\ &=8T\left(\frac{N}{8}\right) + 4O\left(\frac{N}{4}\right) + 2O\left(\frac{N}{2}\right) + O(N) \\ &\quad \vdots \\ & = NT(1) + O(N \log N) \end{align*}\]

여기서 $T(1) = O(1)$ 이므로, FFT의 전체 시간 복잡도는 $O(N \log N)$ 인 것이 증명되었다.

Recursive view vs Convolutive view

• Recursive view
  • 장점
    1. SSM의 State와 Output을 Input sequece의 시간 순서대로 계산 가능하다. → 시스템의 동적 거동을 시계열적으로 직접 분석할 수 있다.
    2. 긴 sequence에서도 초기 데이터의 영향을 무시하지 않게 된다. 따라서 시계열적 데이터에 대해 자연스럽게 inductive bias를 주입할 수 있다.
  • 단점
    1. 순차적으로 데이터를 처리해야 하기 때문에 병렬화(parallelization)가 힘들다. 따라서 학습 속도가 느리다. (Same with RNN)
    2. 너무 긴 sequence를 학습할 때 Vanishing Gradient 또는 Exploding Gradient 문제가 발생할 수 있다. (Same with RNN)
• Convolutive view
  • 장점
    1. 주파수 필터를 통해 data의 지역적인 패턴을 학습하기 때문에 Input data의 지역적인 특징을 잘 포착할 수 있다. → 해석 가능성이 높다 !
    2. 여러 filter의 동시 작동이 가능, convolutional 계산이 가능하기 때문에 병렬 연산이 가능하다. → 계산 효율이 높다 !
  • 단점
    1. Input data에 새로운 data point가 입력되면 SSM의 전체적인 input을 매 번 계산해야 하므로 온라인 학습 또는 Autoregressive context에서 속도가 느리다.
    2. 시계열적인 상태 변화를 직접적으로 볼 수 없기 때문에 시스템의 내부 상태를 추적하기 어렵다.

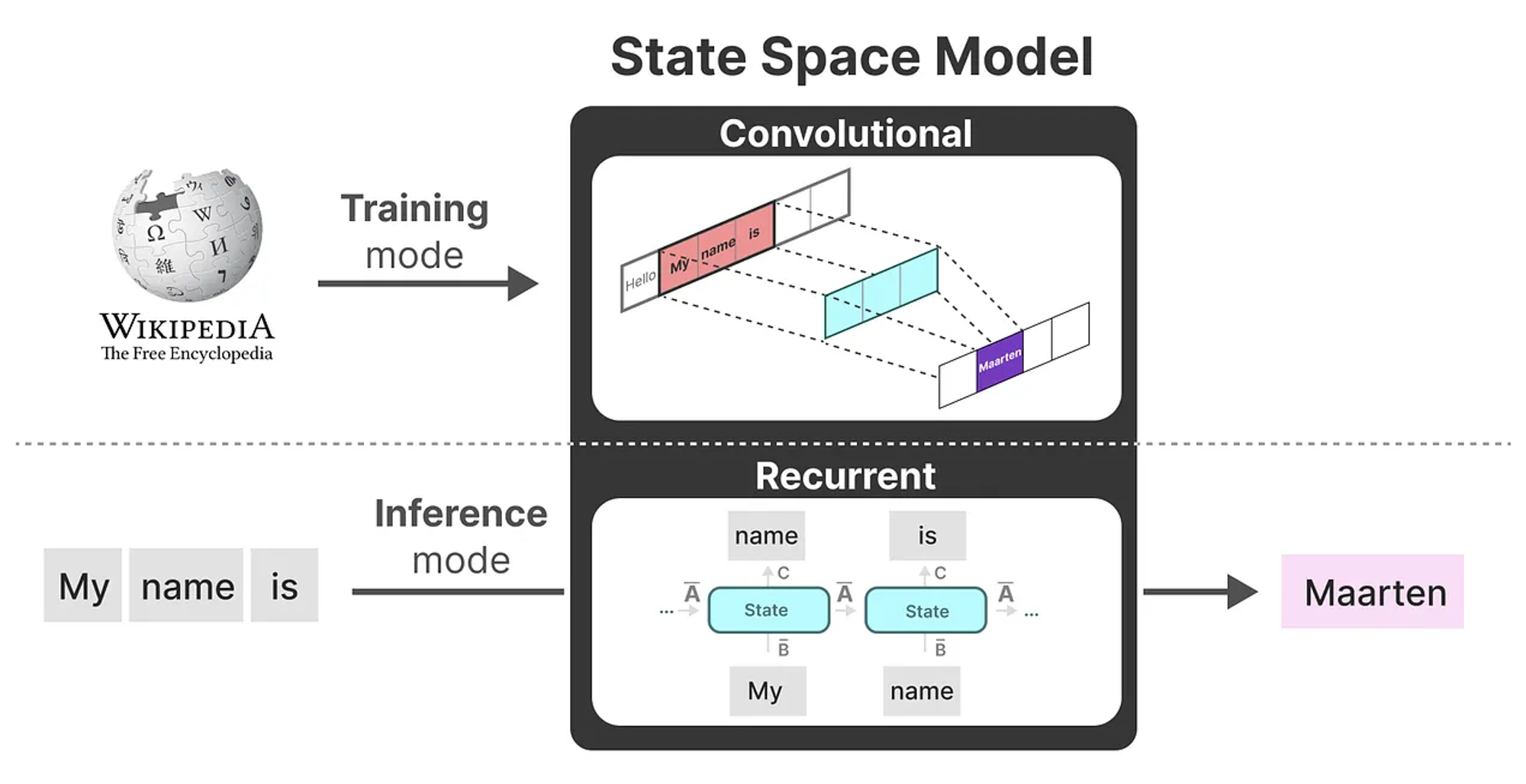
Linear State-Space Layer(LSSL) Modeling

• Idea
  • Training : Convolutional view
  • Inference : Recurrent view 를 이용하자!
• “Linear Time Invariance (선형 시간 불변성, LTI)” ← 매우 중요
  • LSSL에 기반한 SSM의 parameter $A, B, C$는 각 timestep에서 어떤 token이 들어오더라도 동일하다. → 이를 LTI라고 부름
  • 각 token에 대해 가중치를 재조정하는 Attention mechanism과는 대조적임.
  • SSM에 어떤 sequence를 제공하든 간에 $A, B, C$의 값은 동일하다. 이는 즉 “내용 인식이 없는 정적 표현”을 가지고 있다.

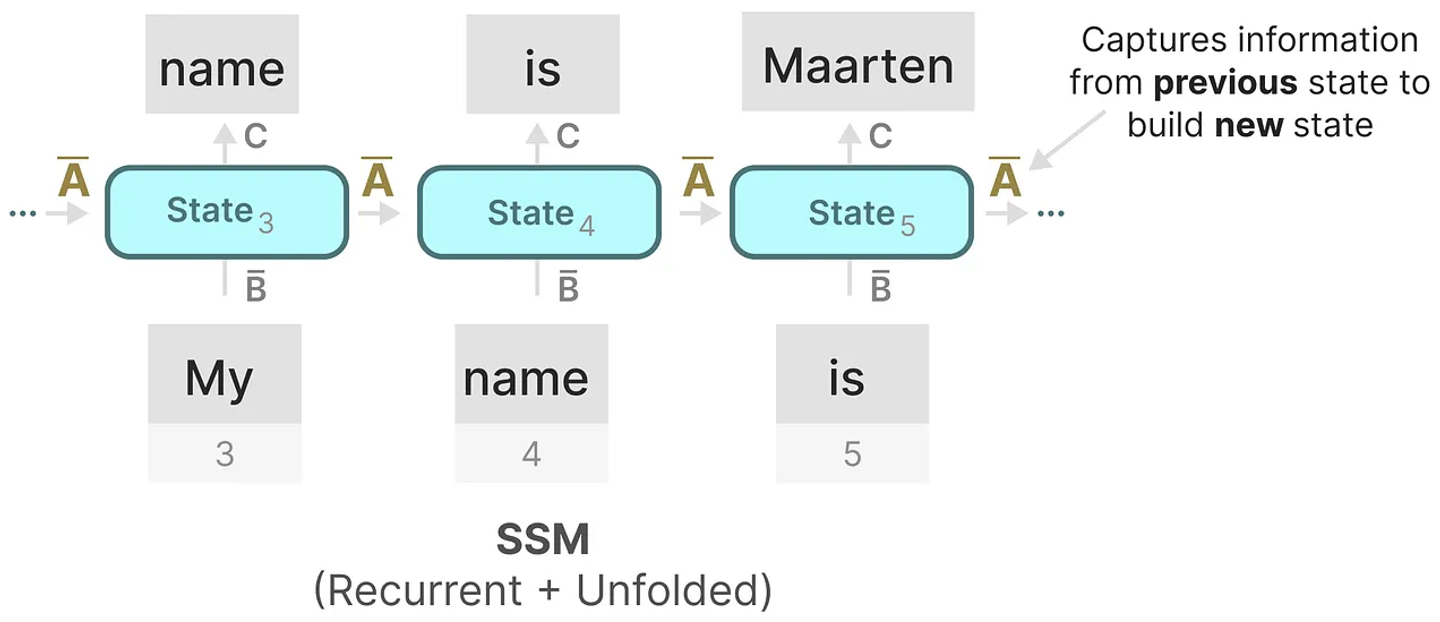
Importance of $A$ matrix

• SSM의 parameter($A, B, C$)를 살펴보면, 계속 Update되는 parameter는 $A$이다.

• $A$ matrix의 의미는 뭘까?

  

  

  → 이전 state에 대한 정보를 포착하여 새로운 state를 구축한다.

  따라서 $A$ matrix를 어떻게 정하냐에 따라 SSM이 얼마만큼(과거~현재 / $0,1,2,…,k$)의 token을 반영할 것인지 결정할 수 있다.

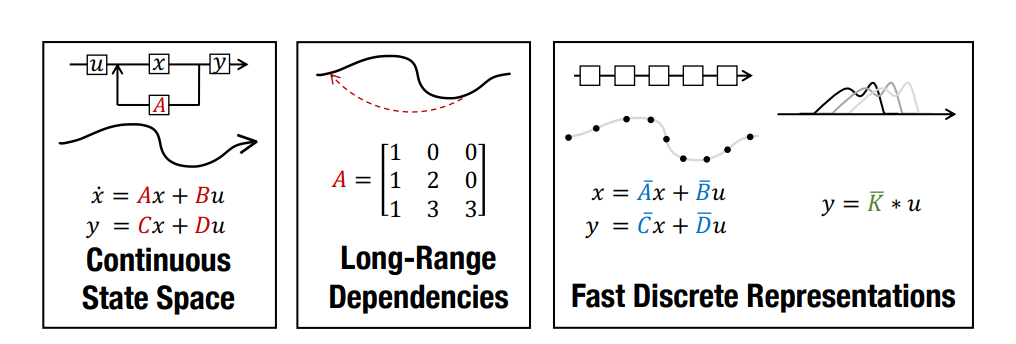
  그러면, 우리는 Long-Context에 대해 과거의 정보를 기억하도록 $A$ matrix를 생성해야 한다. → HiPPO의 발명 !

• HiPPO (High-order Polynomial Projection Operators) - Albert Gu, Tri Dao, et al. (10. 2020)

  • HiPPO-LegS(Legendre State Space) Matrix

    

  • $n$과 $k$의 의미는 뭘까?

    → $n > k$ : everything below the diagonal of matrix $A$

    $n = k$ : the diagonal of matrix $A$

    $n < k$ : everything above the diagonal of matrix $A$

  

  • A를 Learnable parameter가 아니라, 조건에 따른 식으로 직접 design하여 상태 표현 최적화를 이뤄냈다!

  

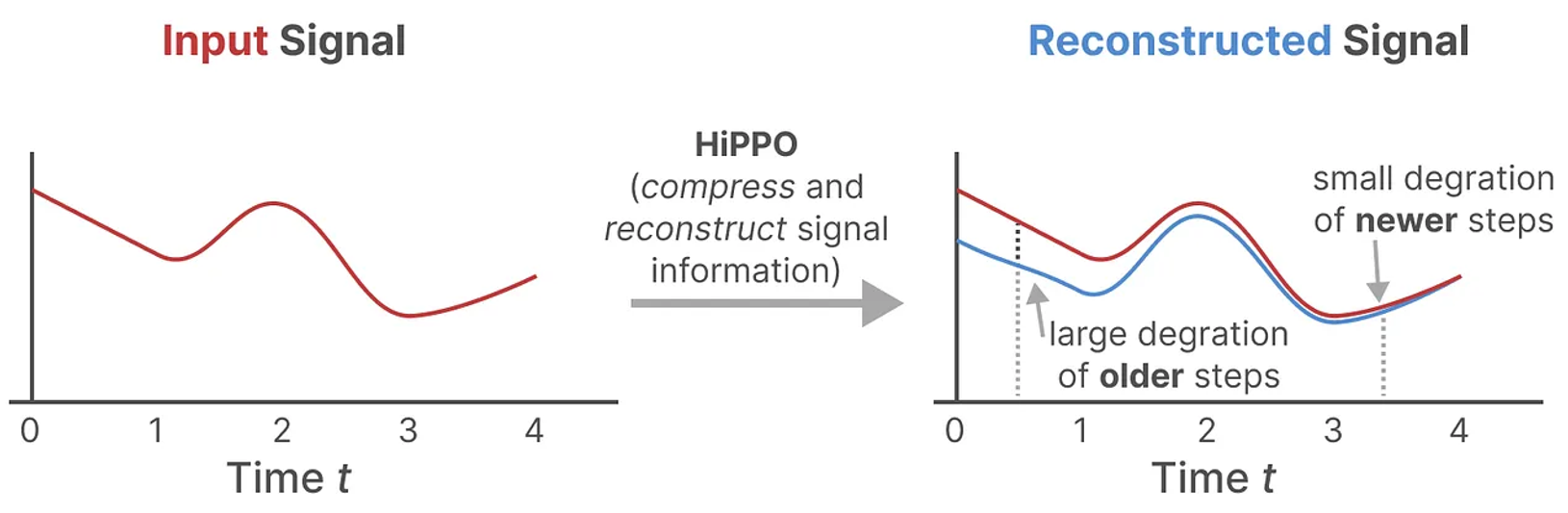
  • HiPPO를 사용하여 구축한 $A$ matrix가 $A$ matrix를 무작위 행렬로 초기화하는 것보다 훨씬 나은 것이 Experiment를 통해 증명됨.

    → 오래된 신호보다 새로운 신호에 더 가중치를 두어 보다 정확하게 data를 재구성한다.

• Structured State Spaces for Long Sequences(S4) - Albert Gu, et al. (11. 2021) - ICLR 2022
  • HiPPO의 $A$ matrix를 SSM에 적용하여 SSM parameter를 update한다.

  

  • S4의 세 가지 구성 요소
    • State Space Model
    • HiPPO for long-range dependancy
    • Discretization for recurrent & Convolutional representations - using Bilinear transform
  • S4에서의 구체적인 A matrix 구성
    • $A$ matrix를 HiPPO matrix로 initialization
    • $A$ matrix를 NPLR(Normal Plus Low-Rank) 구조로 변환 → Diagonalization에 근사 & Low Rank 보정 수행
      • NPLR 형태의 $A = V \Lambda V^* - PQ^*$ ← HiPPO matrix를 다르게 표현한 것임.
        • $\Lambda$ : Diagonal matrix
        • $P, Q$ : Low-Rank matrix
        • $V$ : Identity matrix
      • Woodbury Identity를 통한 Low-Rank 보정
        • \[(\Lambda - PQ^*)^{-1} = \Lambda^{-1} + \Lambda^{-1}P(I - Q^*\Lambda{-1}P)^{-1}Q^*\Lambda^{-1}\]
    • Convolutional 연산에서 Cauchy Kernel 사용 → 계산 복잡도를 줄이고 $A$ matrix의 안정성 향상
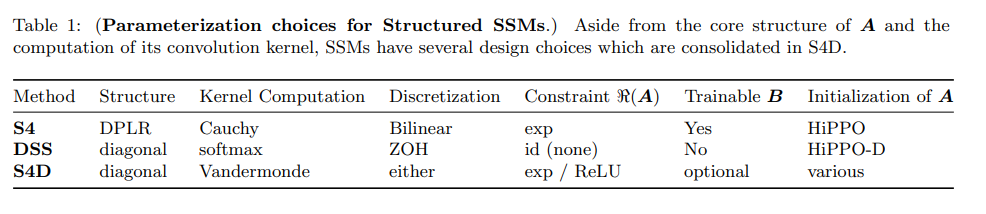
• S4D (Structured State Space with Diagonal state matrix) - Albert Gu, et al. (06. 2022)
  • DiffuSSM에서 SSM architecture의 backbone으로 사용
  • S4에서의 $A$ matrix diagonalization을 보정하여 간단화!

  

  • Continuous sequence의 Discretization에서 ZOH, Bilinear 모두 사용

  

  • HiPPO matrix에서 Low-Rank인 $PQ^*$를 제거하여 단순화 → 완벽한 Diagonalization !
• Mamba - Linear-Time Sequence Modeling with Selective State Spaces (S6) - Albert Gu, et al. (12.2023)
  • Discretization using ZOH

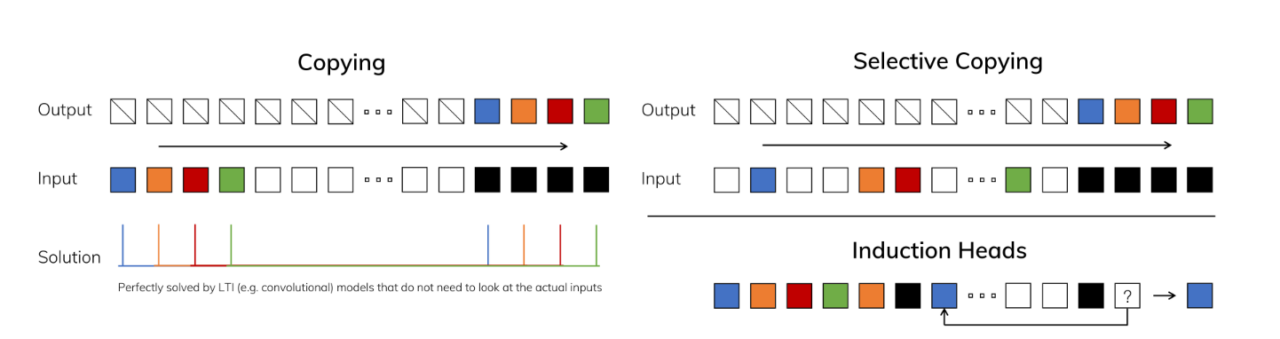
  • Selective Mechanism

    

    • Albert Gu의 기존의 SSM 기반 모델은 $A$ matrix를 비롯한 Parameter update를 고정된 rule로 진행하였다. → input data와 독립적으로 update 진행.

    • Mamba에서는 parameter를 input data에 의존하여 Selective하게 update 진행!

      

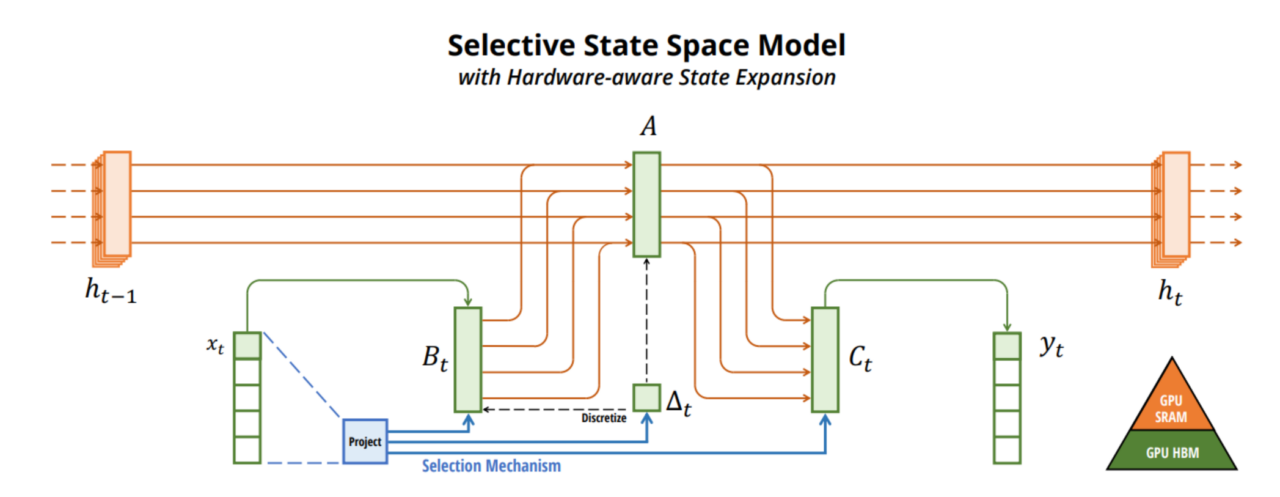
    • 각 Timestep에서의 parameter $A, B, C$를 $A_t, B_t, C_t$라고 한다면
      • $A_t = A + \Delta A(x_t)$
        $B_t = B + \Delta B(x_t)$
        $C_t = C + \Delta C(x_t)$

      $\Delta A(x_t), \Delta B(x_t), \Delta C(x_t)$ : 입력 $x_t$에 따라 동적으로 변화하는 항

    • Selective function
      • $\sigma_t = \sigma(W_s x_t + b_s)$

      $h_t$ : 현재 state

      $\tilde{h}_t$ : 이전 state

      $\odot$ : element-wise multiplication

    • Selective State update : Selective function을 이용하여 state update 진행

      • $h_t = \sigma_t \odot h_t + (1 - \sigma_t) \odot \tilde{h}_t$

        $h_t$ : 현재 state

        $\tilde{h}_t$ : 이전 state

        $\odot$ : element-wise multiplication

    • 그래서 어떻게 Select하는데?

      → 고해상도(high resolution)의 time sequence data에서 중요한 이벤트나 변화(ex. 객체의 경계, 텍스트 등)가 있는 timestep에서 ZOH의 간격을 작게 줌으로써 더 자주 update, 덜 중요한 timestep은 비교적 적게 update!

  • Hardware-aware Parallel Scan Algorithm

    

    • Kernel Fusion
      • SSM training 진행 시, GPU 내부에서 HBM(High Bandwidth Memory)이 아닌 SRAM(Static Random Access Memory, Cache)에서 parameter 저장 및 계산을 kernel로 융합하여 진행
    • Recomputation
      • Forwardpropagation에서 Backpropagation에 필요한 intermediate state(Partial derivation value 등)를 저장하지 않고 Backpropagation에서 재계산 진행. → Memory spatial complexity 최적화

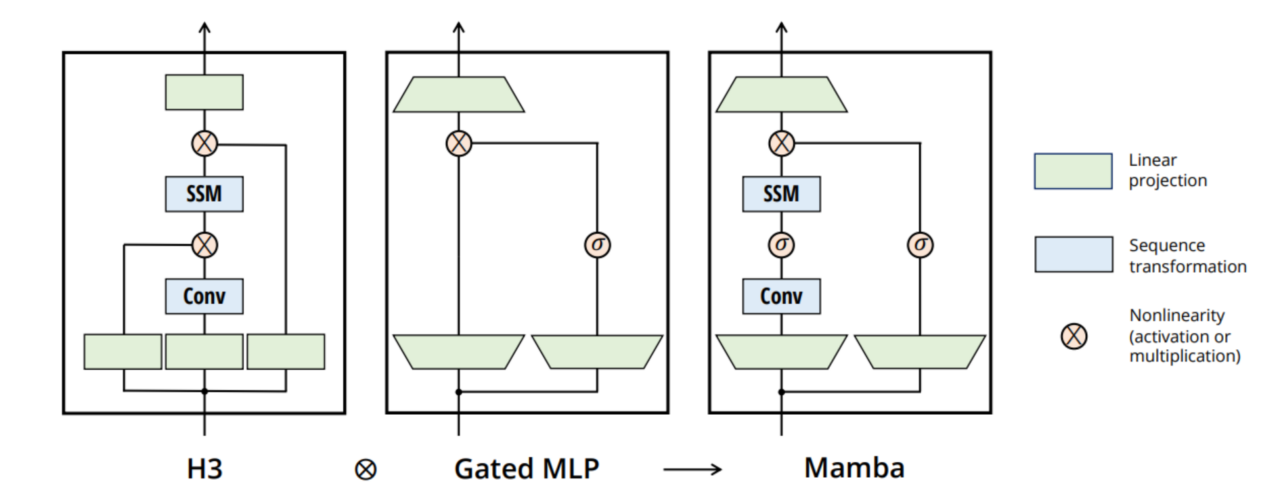
  • Overview of Mamba

    

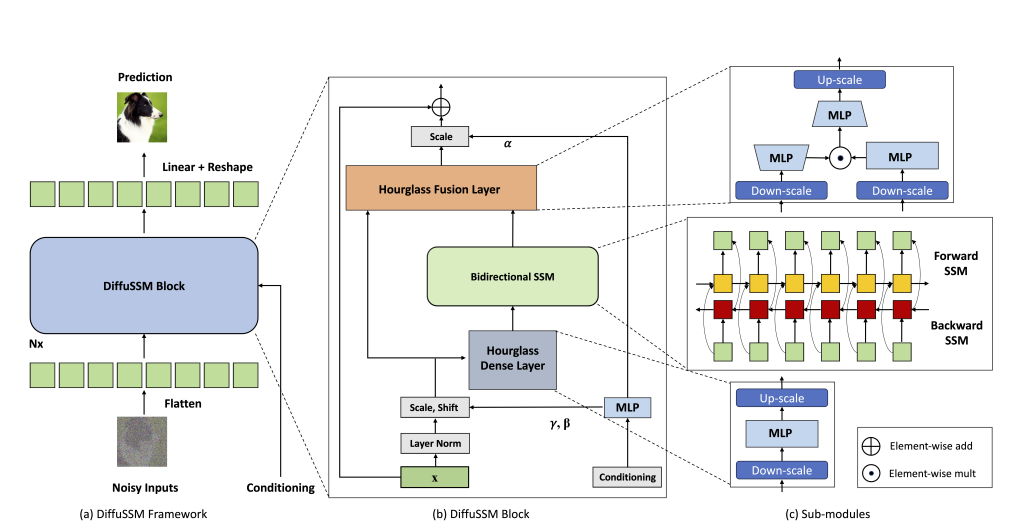
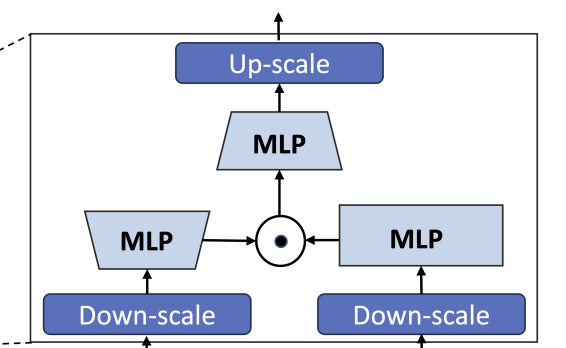
4.2. DiffuSSM Block

DiffuSSM model의 전체적인 Pipeline을 간단히 설명하면 다음과 같다.

1. Input data(ex. 이미지)에 점진적으로 Noise를 추가하여 Forward process 진행, Input sequence 생산
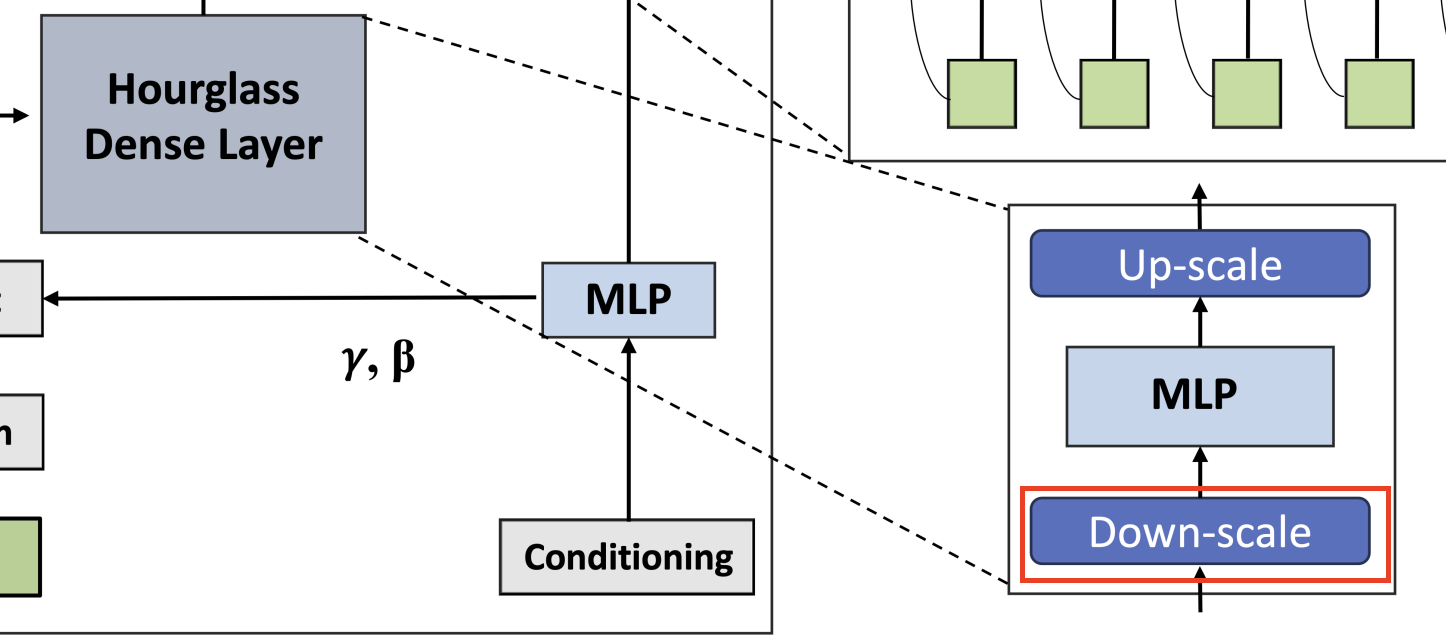
2. Hourglass Dense Layer를 통해 Input sequence를 down-scaling
3. Bidirectional-SSM Block에서 Noise를 제거(복원)하는 Backward process 진행
4. 다시 Hourglass Dense Layer에서 Noise 제거된 sequence를 up-scaling
5. Hourglass Fusion Layer에서 복원된 sequence와 원래 original input sequence를 결합하여 최종 output 생산

맨 처음 들어오는 Input sequence는 길이 $J$와 차원 $D$를 가진 $I$ ($I \in \mathbb{R}^{J \times D}$) 로 가정한다.

Input Sequence Processing

Input sequence $I$를 받아 압축(Down-scale)하고 확장(Up-scale)하여 중간 표현 $U_l$를 생성한다.

• Down-scaling

  

  Down-scaling은 일반적으로 Average Pooling 또는 Linear transform을 통해 수행된다. DiffuSSM은 Linear transform을 이용하였다.

  $U_l = \sigma(W_k^\uparrow \sigma(W^0 I_j))$

  • $I$ : Input sequence ($I \in \mathbb{R}^{J \times D}$)
  • $W_0$ : Input sequence에 대한 Linear transform matrix
  • $W_k^\uparrow$ :Down-scaling을 위한 Linear transform matrix
  • $\sigma$ : Activation function
  • $U_l$ : Down-scaled sequence ($U_l \in \mathbb{R}^{L \times D}$)

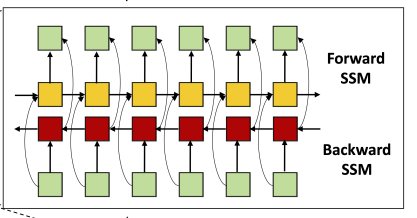
• Bidirectional SSM (using S4D)

  

  Hourglass architecture를 통해 만들어진(Down-scaled) 중간 표현 $U$를 input으로 받아 output sequence $Y$를 생성한다.

$Y = \text{Bidirectional-SSM}(U)$

• $U$ : Down-scaled sequence
• $Y$ : Bidirectional SSM에서 생성된 Output sequence ($Y \in \mathbb{R}^{L \times 2D}$)

여기서 SSM의 backbone model로 앞서 언급한 S4D를 이용한다.

S4D의 matrix definition을 간단히 Recap해보면 아래와 같다.

$A_d = (I - \frac{T}{2} A)^{-1} (I + \frac{T}{2} A)$
$B_d = (I - \frac{T}{2} A)^{-1} T B$
$C_d = C$
$D_d = D$

• Forward S4D

$x_f[k+1] = A_d x_f[k] + B_d u[k]$
$y_f[k] = C_d x_f[k] + D_d u[k]$

• Backward S4D

$x_b[k+1] = A_d x_b[k] + B_d u[k]$
$y_b[k] = C_d x_b[k] + D_d u[k]$

• Output concat

$y[k] = y_f[k] + y_b[k]$

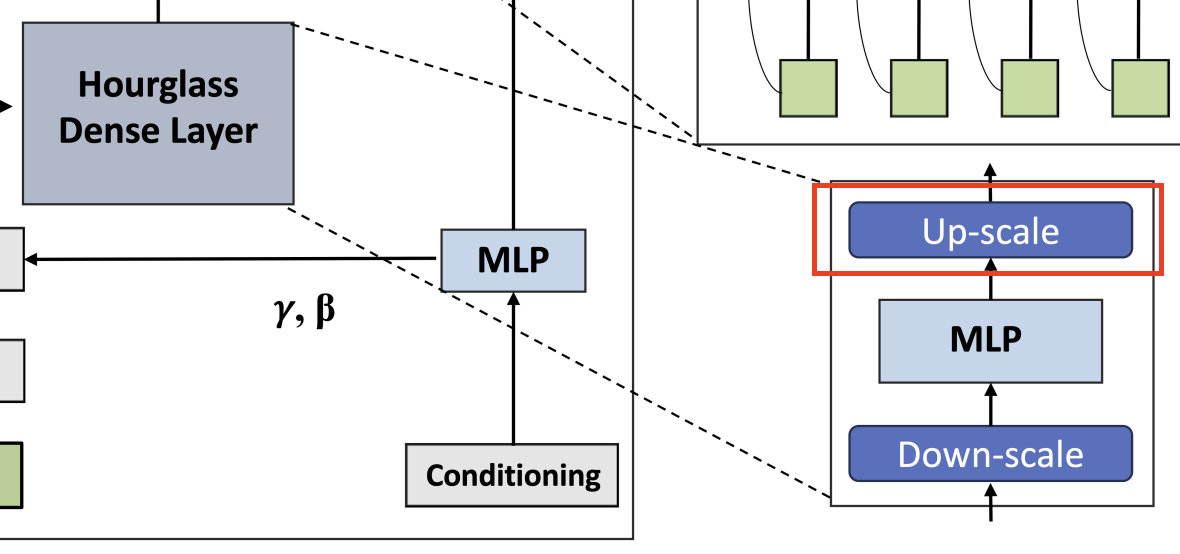
• Up-scaling

  

  Up-scaling은 Bidirectional-SSM의 output sequence $Y$ 를 다시 원래의 길이로 확장하는 과정이다. 이를 통해 저차원 sequence를 다시 고차원 공간으로 변환하여 원래의 sequence length로 복원한다.

  Up-scaling은 Linear Transform을 통해 수행된다.

  $I’_{j, Dm:k:Dm(k+1)} = \sigma(W_k^\downarrow Y_l)$

  • $Y$ : Bidirectional SSM에서 생성된 출력 시퀀스 ($Y \in \mathbb{R}^{L \times 2D}$)
  • $W^\downarrow_k$ : Up-scaling을 위한 Linear transform matrix
  • $\sigma$ : Activation function
  • $I’$ : Up-scaled sequence ($I’ \in \mathbb{R}^{J \times 2D}$)

Output Sequence Processing

• Hourglass Fusion Layer

  Hourglass Fusion Layer에서 Hourglass Dense Layer와 Bidirectional SSM에서 얻은 output을 결합(Element-wise add)하여 최종 output을 출력한다.

  $O_j = W^3(\sigma(W^2 I’_j) \odot \sigma(W^1 I_j))$

  • $I’$ : Up-scaled sequence
  • $I$ : Original Input squence (≠ input image)
  • $W_1, W_2, W_3$ : Linear tranform matrix
  • $\sigma$ : Activation function
  • $O_j$ : 최종 Output sequence

5. Experiment

5.1. Experimental Setup

Datasets

• ImageNet-1k : 1.28m images, 1k class
• LSUN : Church (126k images), Bedroom(3M images)의 두 category
• ImageNet : 256x256 & 512x512, LSUN : 256*256 해상도로 진행

Linear Decoding and Weight Intialization

• Gated SSM의 최종 블록 이후 model은 sequantial image representation을 원래의 original spatial demension으로 decoding하여 noise 및 diagonal covariance의 예측을 출력한다.

Training Configuration

• DiT의 훈련 설정을 그대로 유지하여 모든 model에 동일한 설정 적용
• 지수 이동 평균(EMA)의 감쇠율(decay)를 일정한 상수로 설정
• Pre-trained VAE Encoder를 사용, 훈련 중 paremeter 고정.
• DiffuSSM-XL model의 경우 약 673M parameter를 가지고 있으며, Bidirectional-SSM Block(Gated)은 29 layer로 구성 (similar to DiT-XL)
• Computational cost를 줄이기 위해 Mixed-precision training을 사용하여 훈련 진행

Metrics

• Frechet Inception Distance (FID), sFID, Inception Score, Precision/Recall metric을 사용하여 이미지 생성 성능 평가 진행
• Classifier-free guidance는 명시적으로 언급하지 않는 한 적용하지 않았다.

Implementation and Hardware

• Implemented all models in Pytorch
• Trained them using NVIDIA A100 GPU 80GB * 8, with a global batch size of 256.

5.2. Baselines

• 이전의 최고 모델들과 비교하였음. 여기에는 GAN-style approches, UNet, Latent space에서 작동하는 Transformer가 포함된다.
• 주된 비교 목표는 DiffuSSM의 성능을 다른 baseline과 비교하는 것이다.
• 256*256 해상도 수준의 이미지 생성에 중점을 두었으며, DDPM Framework 내에서 비교하였다.

5.3. Experimental Results

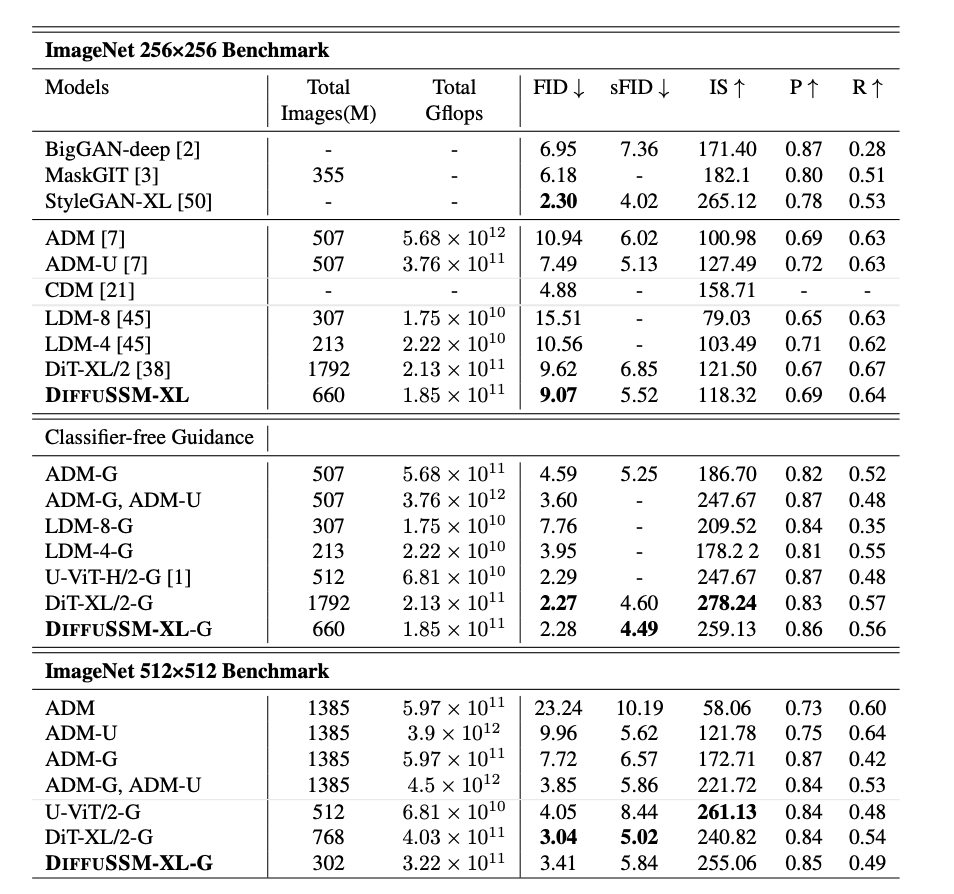
Class-Conditional Image Generation

• 다른 SOTA class-conditional generative model과 비교했을 때 FID와 sFID에서 다른 Diffudion model을 능가했으며, training step 수를 약 3배 줄였다.
• Total Gflops에서 DiT보다 20% 감소한 결과를 보였다.
• Classifier-free guidance를 적용했을 때, DiffuSSM은 모든 DDPM 기반 모델 중 최고 sFID 점수를 기록했으며 space distortion에서 더 robust한 이미지를 생성했다.

Unconditional Image Generation

• LSUN dataset에서의 비교 결과 - DiffuSSM은 LDM과 비슷한 FID 점수를 기록했으며, 이는 DiffuSSM이 다양한 벤치마크와 과제에서 적용 가능함을 보인다.
• LSUN-Bedrooms에서는 총 훈련 예산의 25%만 사용했기 때문에 ADM을 능가하지는 못 했다.

6. Analysis

Additional Images

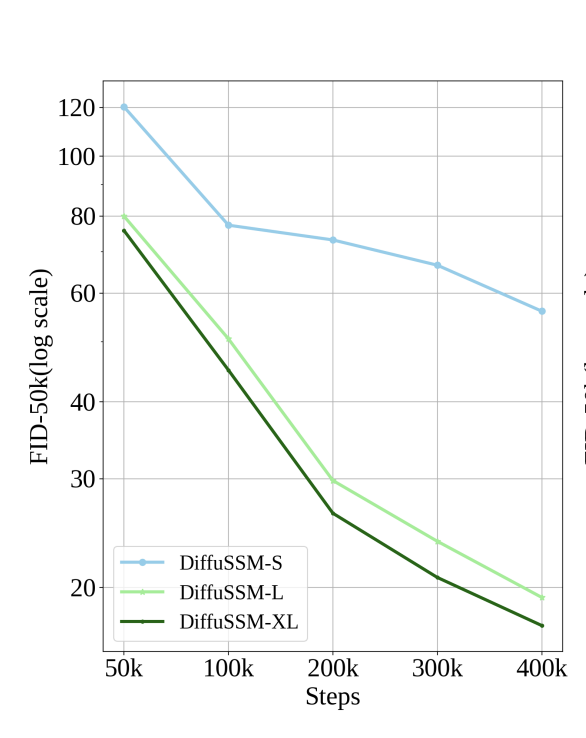
Model Scaling

• 세 가지 다른 크기(S, L, XL)의 DiffuSSM model을 훈련하여 모델 크기 확장이 성능에 미치는 영향을 조정하였다.
  • S : hidden dimension size D(-S/D) = 384
  • L : hidden dimension size D(-L/D) = 786
  • XL : hidden dimention size D(-XL/D) = 1152

  

• DiT 모델과 유사하게, 모델의 크기가 클 수록 FLOPs를 더 효율적으로 사용하며 DiffuSSM의 크기를 확장하면 훈련의 모든 단계에서 FID가 향상된다.

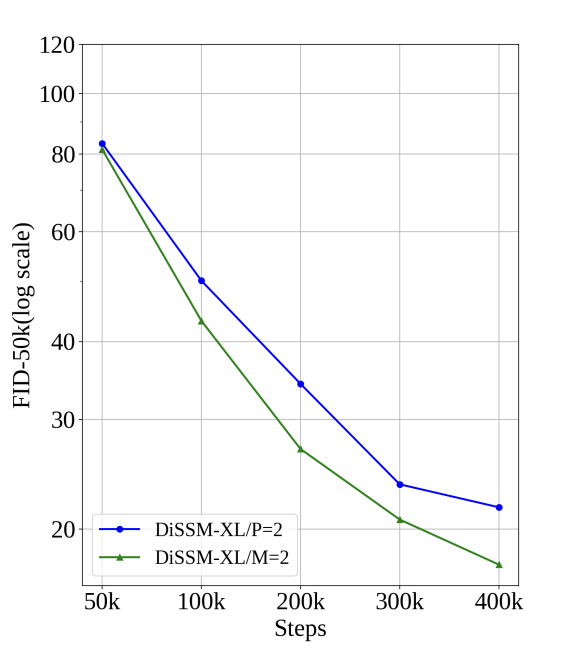
Impact of Hourglass

• Latent Space에서 압축의 영향을 평가하기 위해 다른 샘플링 설정으로 Model training 진행.
• Downsampling ratio $M$ = 2 로 조절한 model과, Patch size $P$ = 2(similar to what DiT has done) 로 조절한 model 두 가지를 실험하여 비교.

Qualitative Analysis

• DiffuSSM의 목적은 hidden representation의 압축을 하지 않는 것이다.
• 세 모델 변형 모두 동일한 batch 크기와 다른 hyperparameter로 400K step의 training을 진행한다.
• Image generating 과정에서 모두 동일한 initial noise와 noise schedule을 class label 전반에 걸쳐 사용했다.

• Image patching의 과정을 제거함으로써 같은 훈련 조건에서 spatial reconstruction 과정의 Robustness를 향상시켰다.
• Computational cost를 대폭 줄이면서도 uncompressed model과 견줄 수 있을 만큼의 image quality를 달성하였다.

7. Conclusion

본 논문에서는 Attention mechanism을 이용하지 않고 State Space Model을 이용하여 Diffusion model을 구성하는 architecture인 DiffuSSM을 소개하였다.

DiffuSSM을 통하여 Representation compression을 이용하지 않고 long-ranged hidden state를 표현할 수 있게 되었다.

더 적은 FLOps를 이용하는 DiffuSSM architecture를 통해, 256x256 해상도의 이미지에서 기존의 DiT 모델보다 더 적은 training을 통해 더 나은 퍼포먼스를 보여주었다. 또한 더 높은 해상도에서도 256x256의 해상도와 비슷한 결과를 보여주었다.

하지만 이 작업에는 몇 가지 제한 사항이 남아 있다.

1. (un)conditional image generation에 초점을 맞추고 있으며 full Text-to-Image의 접근법은 다루지 않는다.
2. Masked image training과 같이 최근에 발표된 접근 방식이 모델을 개선할 수 있다는 점

그럼에도 불구하고, 이 DiffuSSM이 고해상도의 이미지에서 Diffusion model을 효과적으로 학습하기 위해 더 나은 model architecture를 제공한다는 것은 여전히 유효하다.

DiffuSSM은 attention mechanism의 병목 현상을 제거함으로써 hi-fi audio, video, 3D modeling과 같은 long-range의 diffusion이 필요한 분야들에서 응용 가능성을 넓혀 주었다.

Referrence

https://tulip-phalange-a1e.notion.site/05f977226a0e44c6b35ed9bfe0076839
https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mamba-and-state#footnote-anchor-3-141228095
https://angeloyeo.github.io/2019/06/23/Fourier_Series.html#google_vignette
https://angeloyeo.github.io/2020/11/08/linear_algebra_and_Fourier_transform.html#google_vignette
https://hazyresearch.stanford.edu/blog/2022-01-14-s4-3
https://huggingface.co/blog/lbourdois/get-on-the-ssm-train